MATH1115 Algebra Solution

Question 1 10 pts

Consider the homogeneous matrix equation Ax = 0, where

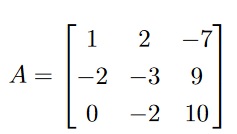
(a) Find the reduced row echelon form of A showing the row operations you use to reduce the matrix. 3 subpts

Solution

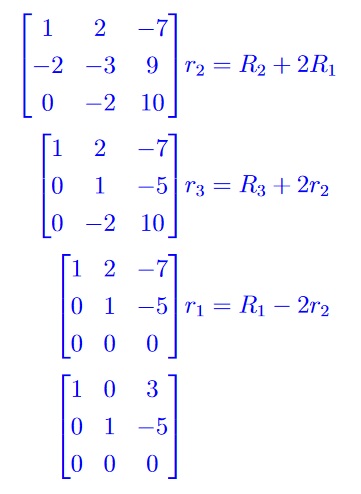
Marking Scheme: 3 points for correct rref and row ops, 2 points for producing a rref, 1 point for some row operations.

Typical errors: Some students didn’t zero out the second entry in the first row.

(b) Find the general solution of Ax = 0 in vector parametric form. 2 subpts

Solution

From the rref we see that x₃ is a free variable. So the basic variables can be written in terms of the free variable: x₁ = −3x₃, x₂ = 5x₃, x₃ is free. In vector form

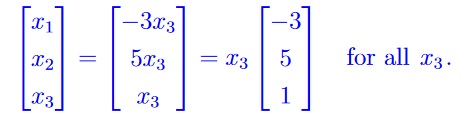
Marking Scheme: 1 point for writing basic variables in terms of the free variable, 1 point for vector form of solution

(c) Describe the solution set geometrically. 1 subpts

Solution

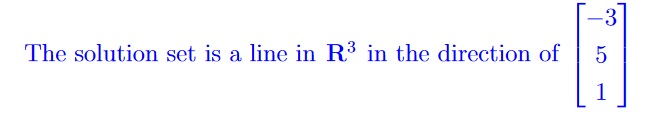
Marking Scheme:

1 point for correct answer.

Typical errors: “The span of a vector” was not an acceptable answer here.

(d) Find all vectors b for which the equation Ax = b is consistent. Write your answer in vector parametric form. 4 subpts

Solution

From part (a) we know the row operations to take A to reduced row echelon form, so we just apply these to the augmented matrix:

Marking Scheme: 2 points for getting the condition b₃+2b₂+4b₁ = 0.

2 points for writing in vector parametric form.

Typical errors: Confusion about how to express b₃ + 2b₂ + 4b₁ = 0 in vector parametric form.

Question 2

In the following questions either give an example that meets the conditions given or explain why such an example does not exist.

(a) Give the reduced row echelon form of the augmented matrix for a linear system with two equations in three unknowns that has (i) infinitely many solutions and

(ii) no solutions. 4 subpts

Solution

Two equations in three unknowns means the augmented matrix is 2 × 4

Marking Scheme: For each of (i) and (ii), 1 point for an echelon of the correct shape, 2 points for correct reduced row echelon form. In (i) only one example is necessary, not both.

Typical errors: Not writing the matrix in reduced row echelon form.

Marking Scheme: Full marks for finding one of the above matrices. Partial marks if the matrix satisfies Ax = 0 but is not in reduced row echelon form.

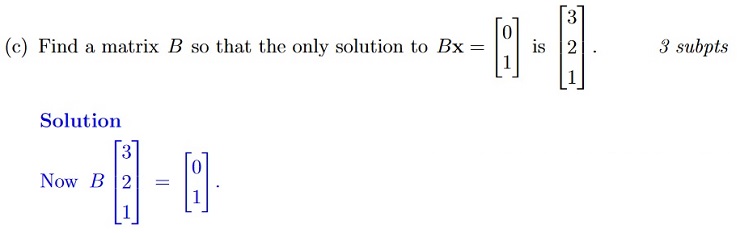
So this system should be consistent. Now consider the

homogeneous equation Bx = 0. As B is a 2 × 3 matrix, we must have an infinite number of solutions to the homogeneous equation, as B must reduce to a form that displays at least one free variable (more columns than rows).

The general solution of Bx = b, as it is consistent, is a particular solution plus all the solutions of the homogeneous equation.

So, we must have an infinite number of solutions. Hence we can not find a 2 × 3 matrix B, which has a unique solution to .

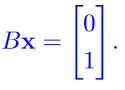
Marking Scheme: 1 point for determining the size of the matrix. 1 point for realising that such a matrix cannot have a unique solution. 1 point for explaining why.

Typical errors: Getting the dimensions of the matrix around the wrong way.

Not seeing that uniqueness was an issue.

Question 3

{`
  If x and y are linearly independent and if z is in Span{x,y} show that {x, y,z} is a linearly dependent set. 3 subpts
Solution z ∈ Span{x,y} implies z = c1x + c2y for some weights c1,c2. Rewriting, this
gives us c1x + c2y − z = 0, and so {x, y,z} is a linearly dependent set.
Marking Scheme: 1 point for writing z as a linear combination of x and y. 1 point for knowing the definition of linear dependence. 1 point for putting the two steps together in a coherent argument.
Typical errors: Failing to see that z = c1x + c2y could be rearranged to give the definition of linear dependence. Quoting the theorem that linear dependence meant one vector was a linear combination of the others as the definition. Not giving enough justification for the reasoning.
If v1,...,v4 are linearly independent vectors in R4, show that {v1,v2,v3} is a linearly independent set of vectors. 3 subpts
`}

Solution

The simplest argument here is to use the contrapositive. So assume {v₁,v₂,v₃} are linearly dependent, i.e. there are some weights not all zero such that c₁v₁ + c₂v₂ +c₃v₃ = 0. By setting c₄ = 0 we see that c₁v₁ +c₂v₂ +c₃v₃ +c₄v₄ = 0 for weights not all zero and so {v₁,v₂,v₃,v₄} are linearly dependent.

Another argument can use the number of pivots in a matrix built from the vectors v_i.

Marking Scheme: 1 point for knowing the definition of linear dependence and independence. 2 points for making a coherent argument.

Typical errors: Saying that because c₁v₁+c₂v₂+c₃v₃+c₄v₄ = 0 has only the trivial solution means c₁v₁ + c₂v₂ + c₃v₃ = 0 has only the trivial solution is not a valid argument.

(c) Suppose A is an m × m matrix with m pivot columns and that {v₁,...,v_p} is a linearly independent set of vectors in R^m. Is {Av₁,...,Av_p} a linearly independent set of vectors? Justify your answer. 4 subpts

Solution

The answer is yes. {v₁,...,v_p} is a linearly independent set so c₁v₁ + ... + c_pv_p = 0 if and only if c₁ = ··· = c_p = 0. Now consider the linear combination d₁Av₁ +···+d_pAv_p. By linearity of matrix multiplication this expression is the same as A(d₁v₁ + ···d_pv_p). The fact that A is an m × m matrix with m pivot columns means that Ax = 0 if and only if x = 0. So we see that

d₁Av₁ + ··· + d_pAv_p = 0 iff

A(d₁v₁ + ···d_pv_p) = 0 iff

(d₁v₁ + ···d_pv_p) = 0 iff

d₁ = ··· = d_p = 0.

Marking Scheme: 1 point for writing down the linear combination d₁Av₁ + ··· + d_pAv_p. 1 point for using linearity of matrix multiplication. 1 point for seeing that Ax = 0 iff x = 0. 1 point for conclusion.

Typical errors: Arguing backwards. Not seeing that the condition on A meant Ax = 0 has only the trivial solution.

Question 4

Let T be a linear transformation defined by matrix multiplication x 7→ Ax where

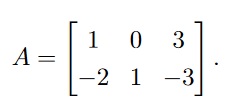
• What is the domain of T ? 1 subpts
• What is the codomain of T ? 1 subpts

Solution

The domain is R³. The codomain is R².

Typical errors: Getting domain and codomain around the wrong way.

(c) What is the range of T ? 4 subpts

Solution

To find the range we must find all vectors b such that Ax = b is a consistent equation. So we row reduce the augmented matrix

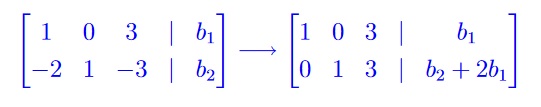
The matrix has 2 pivots so is consistent for all vectors b and the range is all of R2.

Marking Scheme: 1 point for setting up the matrix equation. 2 points for finding the rref. 1 point for seeing that the range is R².

Typical errors: Simply stating that the range is a linear combination of the columns of the matrix was not sufficient.

(d) Find all vectors x such that T(x) = 0. Describe the set geometrically. 4 subpts

Solution

This amounts to finding the general solution of Ax = 0. Using the rref found in

Marking Scheme: 1 point for setting up the matrix equation. 2 points for finding the general solution. 1 point for describing the set geometrically.

Typical errors: Missing the geometric description.