Math midterm 1 solution
(28 Points.) The following are True/False questions. For this problem only, you do not have to show any work. There will be no partial credit given for this problem. For this problem:
- A correct answer gives 4 points.
- An incorrect answer gives 0 points.
- If you leave the space blank, you receive 2 points.
F (a) Five vectors in R5 always span R5.
F (b) If T : Rn → Rm and U : Rm → Rp are both linear transformations, then the standard matrix for the linear transformation U ◦T is n × p.
T (c) If the Row Echelon form of a matrix A has a pivot in every column, then whenever A~x = ~b has a solution, it must be unique.
T (d) The sum of two solutions to the homogeneous problem A~x = ~0 is also a solution.
T (e) If a linear transformation T : Rn → Rm is both one-to-one and onto, then n must equal m.
F (f) Two vectors whose entries are all positive must be linearly independent.
T (g) AssumeT : Rn → Rm is a linear transformation and~v1,. . . ,~vp are vectors in Rn. If {T(~v1),. . . ,T(~vp)} are linearly independent, then {~v1,. . . ,~vp} are also linearly independent.
Each statement below is either true (in all cases) or false (in at least one case).
If false, construct a counterexample. If true, give a justification that carefully notes everywhere you use the definition of “linear (in)dependence.”
- (12 Points.) If ~v1 and ~v2 are linearly independent and ~v1,~v2,~v3 are linearly dependent, then ~v3 is in Span ~v1,~v2 .
- (12 Points.) If u~1 and u~2 are linearly dependent vectors in R2, then one of these vectors must be a constant multiple of the other.
(a) True. We want to show that ~v1 can be written as a linear combination of v1 and v2:
~v1,~v2,~v3 being linearly dependent means that there are numbers a1, a2, and a3 not all zero so that
a1~v1+ a2~v2+ a3~v3 = 0.
Note that a1 , 0 because otherwise we would have
a2~v2+ a3~v3 = 0,
where at least one of a2 or a3 is nonzero – which can’t happen because ~v1 and ~v2 are linearly independent.
So we’re safe to divide through by a1, giving:
a2 a3
~v1+ ~v2+ ~v3 = 0, a1 a1
and thus:
a2 a3
~v1 =− ~v2− ~v3; a1 a1
and so ~v1 is in Span ~v1,~v2 .
(b) True. Because u1 and u2 are linearly dependent, there are c1 and c2 not both zero so that
c1u~1+ c2u~2 = 0.
If c1 , 0, then
c2 u~1 =− u~2.
c1
So u1 is a constant multiple of u2. If, on the other hand, c1 = 0, then c2 , 0, in which case:
c1
u~2 =− u~1,
c2
and thus u2 is a constant multiple of u1.
Consider the Linear Transformation T : R4 → R3 whose standard matrix is:
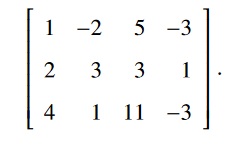
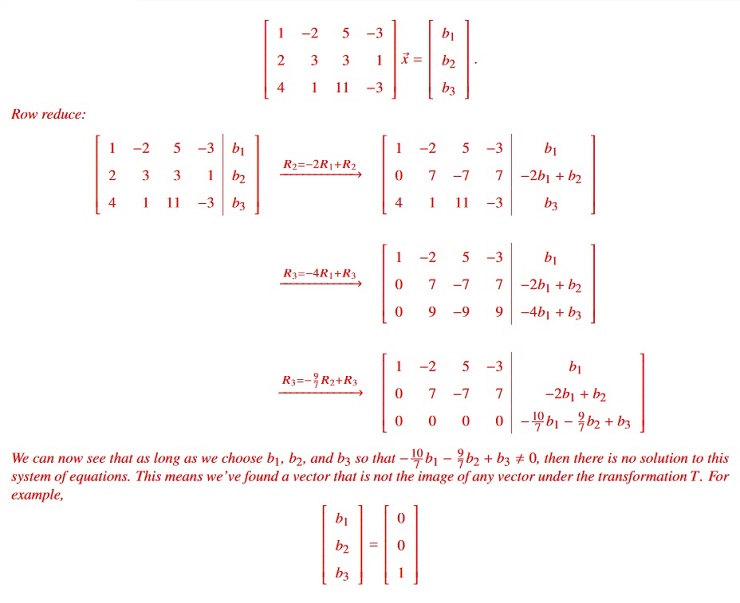
- (18 Points.) Is T onto?
- (6 Points.) If T is onto, solve T(~x) = ~y for a nonzero vector ~y of your choice. If it is not onto, find a vector ~y for which ~y is not in the Range of T.
Reminder: you must show work to receive credit.
Let’s solve this entire problem in one computation (you don’t have to, but it’s more efficient to do so). In particular, we solve, for any ~b:
(24 Points.) Consider the following system of equations (where a and b are constants):
−2x1 + 4x2 = 1
4x1 − ax2 = b
- Choose a and b so that the system has a unique solution.
- Choose a and b so that the system has no solutions.
- Choose a and b so that the system has many solutions.
Let’s row reduce: −.
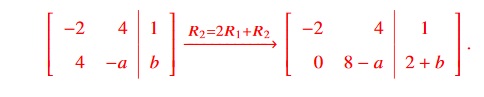
- For a unique solution, choose any a and b so that both the entries that contain a and b are non-zero (so that our system has 2 pivots); a = b = 0 will work.
- For no solutions, choose a = 8 and any b such that 2 + b , 0; b = 0 will work (the second equation would then be 0x1+ 0x2 = 2, which has no solution).
- For many solutions, choose a = 8 and b =−2, making the final row zero, thus giving us one free variable for this system.


