Math 1013 M
Midterm 2
Version 22
Instructions:
- Please write your responses as neatly as possible.
- If you are uploading photos, make sure you can read the images before you submit them.
- If we can’t read your work, we can’t give you points.
How to submit: This is exactly like the crowdmark practice test. You can either:
- Print this test out and complete as normal. When done, scan/photo each question/page and upload to crowdmark using the link they sent you by email.
- Solve each question using your own blank paper. When done, scan/photo each question/page and upload to crowdmark using the link they sent you by email.
- Use a tablet with a stylus to answer questions directly on the pdf file emailed to you by crowdmark. When finished, upload the file to crowdmark using the link they sent you by email.
Code of honour: I am trusting that you are all not cheating for this exam. You are more than welcome to use the notes from class to help you answer the questions (in fact, I encourage it!) But please don’t talk to one another nor should you use the internet to ask for solutions to the problems. I trust in you all.
Exercise 1 (10 points) Find the following limits
Exercise 2 (10 points) Find the following limits
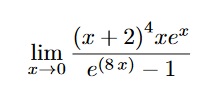
Exercise 3 (10 points) Find the following limits
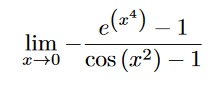
Exercise 4 Differentiate the following:
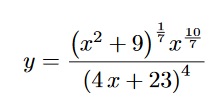
Exercise 5 (10 points) Suppose that s is a function of r. Find d/dr s of the following function:
r4s2 + sin(rs)2 + csc(r + s) = 5
(Bonus - 5 points) Suppose further that r is a function of q. Find dqd s2.
Exercise 6 (25 points)
A 2 meter tall bear is walking in the woods and sees honey flavoured chips strapped to a flashlight hanging from a tree 3 meters above the ground. The bear, smelling honey, decides to raid the chips package and starts walking towards the honey at 3 meters per second. As the bear walks, the flashlight is casting a shadow behind the bear which gets shorter and shorter.
(1) When the bear is 3 meters away from the honey, how fast is the length of his shadow decreasing?
(Assume that the honey chips and the flashlight are at exactly the same point.)
Exercise 7 (5 points) Find a good approximation for
f(x) = arccot(x) at x = 8/9
Exercise 8 (20 points) Using the techniques in class, sketch the curve of the following function.
f(x) = x3 − 18x2 + 81x
Things to include:
- Where does the function cross the x axis?
- What are the critical points? What are the inflection points?
- Where is the graph increasing/decreasing?
- Where is the graph concave up/down?



