Linear Programming Quiz 5

1. In a linear programming problem, the objective function and the constraints must be linear functions of the decision variables.

True

2. Does the following linear programming problem exhibit infeasibility, unboundedness, alternate optimal solutions or solvable with one solution?

Max 3X + 3Y
s.t. 1X + 2Y > 16
1X + 1Y > 10
5X + 3Y > 45
X , Y > 0

Unboundedness

3. Quill Manufacturing Business makes two models of marking pens. An unlabeled graph for this problem and the requirements for each lot of pens in the three manufacturing departments are given below. All three departments are necessary in the production of both types of pens. The profit for both types of pen is $1000 per lot.
   Which constraints are binding?

Ink Assembly and Molding Time

4. Quentin Magic Brown manufactures sports shoes and wants to maximize the company's profits. The company makes two types of sport shoes, Airwalkers and Bouncy Basketball shoes. The company earns $10 profit on each pair of Airwalkers and $18 profit on each pair of Bouncy Basketball shoes. The manufacturing process includes cutting the materials on a machine and having workers assemble the pieces. Each pair of Airwalkers requires 3 minutes of cutting time and the Bouncy Basketball shoes require 2 minutes. The machines that cut the material can run at most 1200 minutes a week. Each worker takes 7 hours to assemble a pair of Airwalkers and 8 hours to assemble a pair of Bouncy Basketball shoes; the maximum number of hours available is 3500 per week. Determine the maximum profit for this problem?

$7875

5. A linear program has been solved and sensitivity analysis has been performed. The ranges for the objective function coefficients have been found. For the profit on X, the upper bound is 80, the lower bound is 60, and the current value is 75. Which of the following must be true if the profit on this variable is lowered to 70 and the optimal solution is found?

The solution values for all the decision variables will remain the same

6. Quality Bike Maps has produced four map designs for the local area. A limited amount of time (in minutes) is allocated to the printing, cutting and folding of each map. Additionally, at least one thousand of map designs A, B, and C must be printed. The profit per map is $1 for A and B and $2 for C and D. Use the Report below and assume the current objective function value is $10,166.67, to determine the new objective function value if the profit for Map D increases by $1.

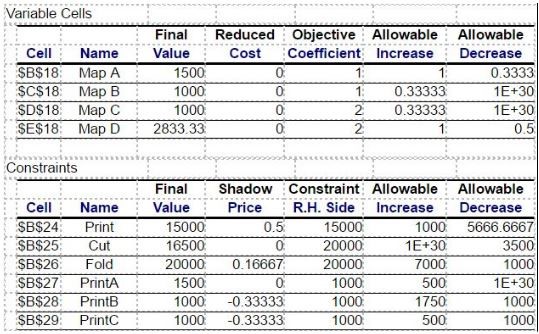
13,000.00

7. Quality Bike Maps has produced four map designs for the local area. A limited amount of time (in minutes) is allocated to the printing, cutting and folding of each map. Additionally, at least one thousand of map designs A, B, and C must be printed. The profit per map is $1 for A and B and $2 for C and D. Using the Report below, which constraint(s) are binding?

Print, Fold, Print B and Print C

8. Using the output below, how much is each additional unit of skilled labor worth?

$5.570