Assignment Help with Linear Equations, Graphs and Slope

Linear Equations Introduction
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable. A linear equation is special because:
- It has one or two variables.
- No variable in a linear equation is raised to a power greater than 1 or used as the denominator of a fraction.
- When you find pairs of values that make the linear equation true and plot those pairs on a coordinate grid, all of the points for any one equation lie on the same line. Linear equations graph as straight lines.
One Variable:
A linear equation in one unknown x may always be rewritten
ax=b
If a0, there is a unique solution
x=b/a
If a = 0, then either the equation does not have any solution, if b 0 (it is inconsistent), or every number is a solution, if b is also zero.
Two variables:
A common form of a linear equation in the two variables x and y is Y=mx+b
where m and b designate constants (parameters). The constant m determines the slope or gradient of that line and the constant term b determines the point at which the line crosses the y-axis, otherwise known as the y-intercept.
Different forms for 2D equations:
- General (or standard) form
- Slopeintercept form
- Pointslope form
- Two-point form
- Intercept form
- Matrix form
- Parametric form
- 2D vector determinant form
Graph for linear equation:
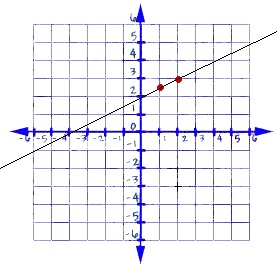
Let's draw the graph of this equation.
y = 1/2 x+ 2
- Find the x and y values of two points that satisfy the equation
- Plot each point, and then draw a line through the points.
We can start with any two x values we like and then find y for each x by substituting the x values into the equation. Let's start with x = 1.
| Value of x | y=1/2 x +2 | Value of y |
|---|---|---|
| 1 | y=1/2*1+2=1/2+2 | 2.5 |
| 2 | y=1/2*2+2=1+2 | 3 |
Let's plot these points and draw a line through them.
Slope: The slope intercept form of a linear equation has the following form where the equation is solved for y in terms of x:
y = a + bx
b is the slope
a is a constant term. It is the y intercept, the place where the line crosses the y axis.
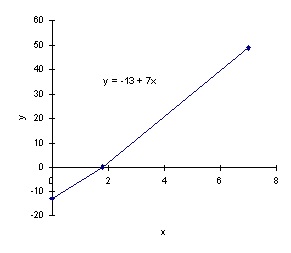
Example
y = -13 + 7x
This equation is in slope intercept form. The y intercept is (0,-13) and the slope is 7.