Lab 125 Conservation of Energy in Spring-Mass System

For the equation below, h₀ is the distance between the motion sensor and the spring with no motion. When there is no motion, the distance from the detector is measured as h.

E_mech = 1/2mv² + 1/2k(h-h₀)² + (mg)²/2k

Because (mg)²/2k is a constant, the sum of the first two terms on the right side of the equation directly above must remain the same for equilibrium to be conserved.

For part 1 of the experiment, we measured the spring constant k. For part 2 of the experiment, we experimentally verified the conservation of mechanical energy of a spring-mass system. The motion sensor was used to detect oscillation and a graph of distance h with velocity v. time for the system was obtained. Using manual calculation and verifying manual calculations with software generated data, we were able to confirm energy is conserved at every point in time for the vertically oscillating spring-mass system.

3. Experimental Procedure

Part I. Spring Constant Measurement

1. The weight hanger was massed to be 84.86 grams. It was then hung on the spring.
2. We logged onto the computer, connected to USB cable of the 850 Universal Interface to a USB port on the computer, and connected the AC adapter power cord to an electrical outlet under the lab table. The green button at the corner of the interface was pressed.
3. The computer file labeled “Lab 125 Spring Mass System” was opened up.
4. The distance from the weight hanger to the sensor was measured under a condition of no motion.
5. The program generated a position v. time graph. The position data was averaged using tools in the tool bar on top of the graph. The position value y₀ was recorded in Data Table 1.
6. Mass was added in increments for each trial to expand the spring. Position y_n was repeatedly measured and recorded each trial, n representing the trial number. Displacement of the spring was calculated each trial, obtained with y₀ – y.
7. A graph of the spring force (in N) v. displacement (in m) was graphed and fit with a regression line. The slope was the spring constant k (in N/m).

 Part II. Verification of Conservation of Mechanical Energy of a Spring-Mass System

1. The same setup as part 1 was maintained.
2. “Part-IIA” in the program was opened up.
3. A 250g mass was added to the weight hanger and the equilibrium position was measured with the sensor and recorded in Data Table II.
4. The spring was started vertically oscillating on an amplitude of about 5 cm within the optimum range of the motion sensor.
5. “Record” was clicked on the program interface and a graph of position v. time and a graph of velocity v. time for the same data were generated.
6. Using the “Show Coordinates” tool, the values of position (h) and velocity (v) at crest, trough, and equilibrium positions on the plot were obtained.
7. The total mechanical energy at the specified points was then calculated using the given equations. The three values of mechanical energies were compared.
8. All data was recorded in Data Table II.
9. The capstone software was used to compute the mechanical energy at every point. The generated data was used to confirm our manual calculations.
10. Results (Data and Conclusion)

4.1 Experimental Data

Table1

M (mass of weight hanger) = 0.08486 kg

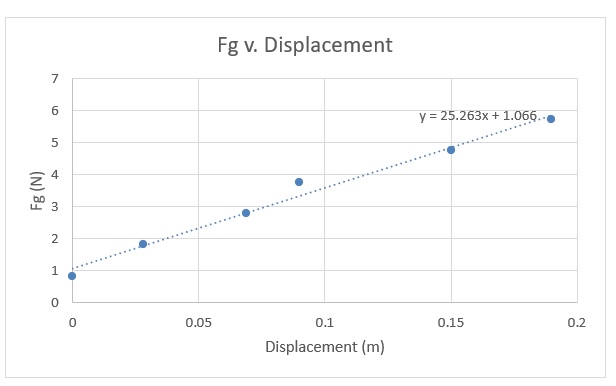
As can be seen in the graph, k has been estimated to equal 25.263 N/m.

Table2

m = M + 0.25 kg = 0.33486 kg

(h₀) = 0.413 m

Equilibrium Position

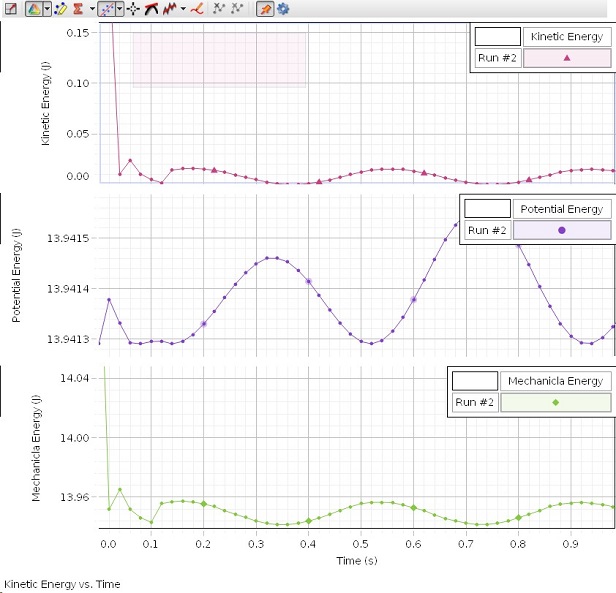
Capstone Program Graph

4.2 Calculations

Table 1 calculations were relatively simple. Since y_i was measured to be 0.503 m, to find further y_ns, I simply did y_n – y_i to get each of the displacement values in the table. Since the spring system in part 1 was at rest, the relationship F_g = F_s would hold true, meaning F_g = kx. I then graphed values of F_g v. displacement to get a linear graph with a slope of value 25.263 N/m. r

Table 2 calculations were relatively simple as well. Displacement and velocity were read off of the screen for 3 points, point 1 referring to a peak of position, point 2 referring to a position of near 0 displacement, and point 3 referring to a trough of position. Using this data, I then plugged in values of mass, velocity, spring constant, displacement and energy values to get the remaining three columns of data. Sample calculations for Point 1 are as followed:

Sample KE calculation:

KE = mv²/2

KE = (0.33486 kg)( -0.004 m/s)²/2

KE = (0.33486)(1.6 x 10^-5)/2

KE = 2.7 x 10^-6 J

Sample PE calculation:

PE = kx²/2 + m²g²/(2k)

PE = (25.263 N/m)( 0.037 m)²/2 + (0.33486 kg)²(9.81m/s²)²/(2(25.263 N/m))

PE = (25.263)( 0.0014)/2 + (0.1121)(96.24)/50.53

PE = 0.231 J

Sample ME calculation:

ME = KE + PE

ME = (2.7 x 10^-6 J) + (0.231 J)

ME = 0.231 J

4.3 Error Analysis

There was some error in the program generating Mechanical Energy measurements. ME reached a max value of 13.952 J and a minimum value of 13.94 J. Percentage difference between the two values is calculated below:

E_abs = max value – min value

E_abs = 13.952 J – 13.94 J = 0.012 J

13.952 J ± 0.012 J

E_rel = E_abs /min value

E_rel = 0.012 J /13.94 J

E_rel = 0.1%

5. Discussion

The prediction of total energy was not close at all to the experimental result. My group did not perform the lab correctly, forgetting (in Part II) to input the k constant and mass of the hanging mass into the program for accurate graphs of PE, KE, and ME. Had we performed the done so, the results probably would have been a lot more accurate as a reflection of experimental results. Knowing that, the error calculation between the maximum and minimum values of the returned ME graph from the program was not really applicable to our experiment, but the relationship between KE, PE, and ME in the graph would hold true even with different k constant and mass values. Were the experiment to be performed again, I would suggest more closely monitoring the experimental procedure and making sure that all technical details are taken care of.

Besides that, sources of error could have included errors of reading the measurements on the screen, error in manually recording and measuring data, error in setting up the experiment, using the wrong weight amounts, failing to check for possible defects in equipment like a broken spring or weight hanger, among other things. Systematic error could have occurred because supposing the massing device was not zeroed properly, or the sensor was tilted a little askew from the line of motion, results could have been skewed up or down, depending. Random errors could have occurred as well. Part I was supposed to be a spring-mass system under equilibrium, and sometimes, the system shook a little. Some trials were not performed as carefully as others, and it was difficult to make sure that for Part II, the spring-mass system oscillated completely vertically. For that reason, there could have been an increased error with results when motion was added in the equation, either motion in the wrong directions, or increased motion when there should have been none.

Looking at the mechanical energy graph generated by the capstone program, there is a little variance in the total mechanical energy. The difference is not big, the line of data is just a little variable. Percentage difference was calculated to be 0.1% as seen above in the error section, but as explained before, this data is not really applicable to our experiment because we failed to input a k constant and the mass as needed for accurate KE, PE, and ME graphs.

6. Conclusion

As this lab is concluded, I now know how to test for the k value, total mechanical energy, kinetic energy and potential energy of a spring-mass system using a force sensor. I also know how to verify the conservation of mechanical energy in a spring-mass system. We did not perform the second part of the lab correctly, but in any given spring-mass system, the relationships in the KE, PE, and ME graphs will be the same under simple harmonic motion. Since I performed the theoretical calculations and understand how they work, I have come through with an understanding about how to accurately perform the lab, were it to be done again and of the underlying concepts the lab tries to teach. Next time, I would be sure to look more closely at the procedure and take precautionary measures that nothing is missed.

For this lab, we performed 5 trials for Part 1 of the lab to observe the relationship described by Hooke’s Law, where F_s = -kx. Since under a condition of equilibrium a mass- spring system doesn’t move, the forces balance out, mg = -kx. So F_g = kx, which was graphed using Excel, the slope of the line determined to be the spring constant. Hooke’s Law was thus confirmed. For Part II of the experiment, various equations were confirmed to check for the relationship between KE, PE, and ME. Using a system of an oscillating mass, position and velocity measurements were taken at 3 positions, when the peak of position was reached, when the average of position was reached, and when the trough of position was reached. Using equations KE = mv²/2, PE = kx²/2 + m²g²/(2k) and ME = KE + PE, I manually calculated the given energy values and was able to confirm the relationship between these three equations, where under every point of motion in an energy curve for an oscillating spring-mass system, KE + PE = ME, and energy is conserved.