div>

Group Theory Introduction

Group theory is the study of algebraic structures. This group theory deals with well known algebraic structures like rings, fields, and vector spaces. Group theory has influenced many parts of algebra. The two main branch of the group theory are linear algebraic groups and Lie groups. Various physical systems, such as crystals and the hydrogen atom, can be modelled by symmetry groups.

Main classes of the Groups are as following:

• Permutation groups
• Matrix groups
• Transformation groups
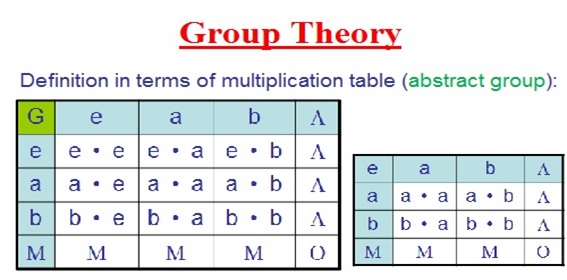
• Abstract groups
• Topological and algebraic groups

---

Group Theory Assignment Help By Online Tutoring and Guide Sessions at AssignmentHelp.Net

---

The axioms (basic rules) for a group are:

• CLOSURE: If a and b are in the group then a b is also in the group.
• ASSOCIATIVITY: If a, b and c are in the group then (a b) c = a (b c).
• IDENTITY: There is an element e of the group such that for any element a of the group a e = e a = a.
• INVERSES: For any element a of the group there is an element a-1 such that
  aa^-1 =e
  a^-1 a = e

Theorem:

G = A * B ->
A & B are invariant subgroups of G
G/A ≈ B, G/B ≈ A

Proof:

g = a b -> g a' g¹ = a b a' b¹ a¹ = a a' b b¹ a¹ = a a' a¹ ∑ A

A is invariant ; dido B.

G = { a B | a c- A } -> G/B ≈ A & similarly for B

Example: S₃

H = { e, {123}, { 321 } } is invariant. Let Hi = { e, (j k) } ( i,j,k cyclic )

Then S₃/H ≈ Hi but S₃ ≠ H * Hi