Folding Block Puzzle Game

Problem - Folding Block (Hand-Written) (15 points)

"Folding Blocks" is a puzzle game, in which you need to unfold the blocks in order to fill the whole space. When you unfold a block, the block is extended with the same size to the unfolding direction. You can play the 2D version of this game here: https://www.crazygames.com/game/folding-blocks-puzzle.

Here we play the puzzle on a 1D board, where the whole space can be viewed as a line illustrated below. If a 2-length block initially fills 3-4 positions, and now we unfold it to the right side, it will fill 3-6 positions of the board.

Now given the length of the board, denoted as N, and the initial status (each block's length and position), please decide whether this puzzle can be solved. Note tht the given position of the block is its leftmost side and a puzzle is solved once all positions are filled after unfolding without overlapping or out-of-board blocks.

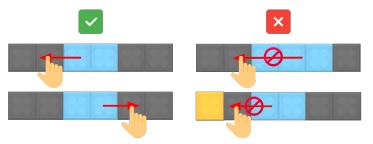
Fig 1. You can unfold the block to the left or right, but you cannot overlap other blocks or make blocks out of board when unfolding.

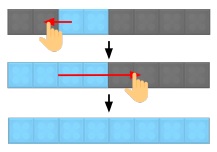
Fig 2. There's an example puzzle and solution.

1. Let's start with a special case which has only a block on the board intitially. Derive a method which can determine whether the problem is solvable in constant time. (Assume the time complexity of a logarithmic operation ()log is O (1)) (2 Points)
2. Assume there is only one block on the board initially. Design a O(logN) algorithm to output the sequence of unfold operations that solve the puzzle if it is solvable. (1 point)
3. Assume there is only one block on the board and the distance between the block to the left and right boundaries are d₁ and d₂ respectively. Prove that there re O(d₁+d₂) possibilities of the status after unfold operations. You can think of a status as a binary array representing whether each position is occupied. (3 points)
4. Let's now consider the general case which can contain more than one block initially. Please design a DP algorithm to solve the problem in O(N) time. (5 points)
5. Explain your algorithm in (4) in terms of the properties of overlapping sub-problems and optimal substructure. (2 points)
6. Prove that the time complexity of your DP algorithm is O(N). (2 points)