FINC3017 Asset Allocation and Portfolio Construction Sample Assignment

FINC3017 Asset Allocation and Portfolio construction

Report 1

Assignment Id: FINC3017

1.0 Introduction

The following report seeks make a summary of the maximal weights of a portfolio created from five equity EFTs. The five EFTs are: eFunds Australian Large-(ALARGE), ASMALL (eFunds Australian Small-Caps), US100 (eFunds US Top 100), ASIA100 (eFunds Asia (ex-Japan) Top 100) and eFunds Emerging Markets Top 500 (EM500). Upon creation of the optimal Portfolio for the two investors (Kendall and Morgan), the expected performance for each investor is calculated and necessary advisory offered to the investors. From the provided expected returns and the volatility of the five EFTs, we are expected to calculate the expected utility that each investor will attain upon investing in a single EFT and make recommendations regarding the best Single EFT to invest in. The provided data is also used to calculate the optimum weights for a portfolio which will maximize the utility of the two investors. To come up with optimal risky portfolio, we will use the Markowitz portfolio theory. The transaction costs taxes and the potential fees have not been put into consideration in this case.

• Expected Utility

The utility function is U=E (R) -where A is represents the risk aversion coefficient for the investor. Kendall Lee has a risk aversion coefficient is 6.5 while that of Morgan Numer is 3.5. The expected utility of the two investors is calculated as follows.

Kendall Lee Utility function is = E (R) -

The expected Utility of Kendall (E ()) of the five scenario when he invests on each single EFTs is

From the calculated expected utility, Kendall Lee chooses the EFT with the optimal utility. US100 (eFunds US Top 100) has the highest expected utility of the five EFTs.

Morgan Numer utility function is = E (R) -. The five scenarios in case where the Morgan invests in each EFT presented in the table below. From the expected utility of Morgan, ASMALL (eFunds Australian Small-Caps) has the highest expected utility of 0.106568. If Morgan is to invest in a single EFT, he will have to choose an asset which maximizes the highest expected value. In this case Morgan invests in ASMALL (eFunds Australian Small-Caps).

• Optimal Risk portfolio Construction

In modern portfolio theories, creating a mix of highly volatile assets (assets with high standard deviation) and low volatile assets (assets with lower standard deviation) helps to reduce the risk associated with a portfolio. This aspect of creating a combination of assets with different risks in different sectors and geographical areas is called diversification. Diversification of portfolio helps reduce the diversifiable risks and boost the return of an investment.

Based on the importance of diversification it is advisable for Kendall and Morgan to consider it. There is need to construct a portfolio which will generate high returns and help reduce the risks associated with investing in a single EFT. To construct a portfolio with the optimal risk, the Markowitz Portfolio theory is used. Theses portfolio utilizes covariance matrices to create a portfolio.

The Variances and standard deviations of the five EFTs are presented below.

From the standard deviation and the correlation matrix a variance covariance matrix can be calculated

The correlation matrix is presented below as the Matrix B

The variance-covariance matrix is obtained by A*B*A. The variance-Covariance Matrix obtained from the above operation is given below.

To calculate the portfolio allocation to each asset EFTs using Markowitz theory we will use the excel solver and maximize the Sharpe ratio which on the hand maximizes the utility of each investor.

Kendall Optimum Portfolio

To create this portfolio the following assumption were made.

• The initial weights of the EFTs are all assumed to be equal
• The sum of the weights is 1
• All the weights of the portfolio formed sought to have all the EFTs included with the lowest range [0.05,0.4]

Under the above conditions the optimal portfolio for Kendall has the following weights.

The variance-covariance matrix as calculated before is given

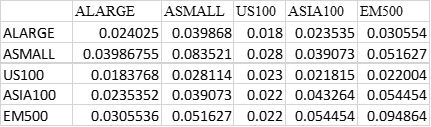
The weights are calculated using solver as given below

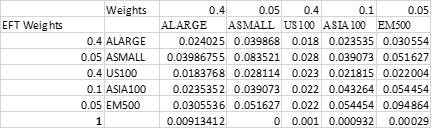
From the above table the portfolio consists of 40% ,5%,40%,10%,5% for ALARGE,ASMALL,US100,ASIA100 and EM500 respectively. This portfolio is the one that will optimize the Sharpe ratio which also means that the utility of Kendall is maximized. The portfolio mean and standard deviation are calculated using the weight matrix and the EFT expected return matrix.

For the weights to be determined, the Sharpe ratio is maximized

For the case of Morgan, the conditions for constructing the optimum portfolio was under the following conditions.

• The initial weights of the EFTs are all assumed to be equal
• The sum of the weights is 1
• All the weights of the portfolio formed sought to have all the EFTs included with the lowest range [0.1,0.5]

Morgan optimum portfolio is determined below

Morgan optimum portfolio weights are 20%, 10%, 50%, 10% and 10% for the EFTs ALARGE, ASMALL, US100, ASIA100 and EM500 respectively. The portfolio mean, standard deviation and the Sharpe ratio as well as the expected utility of the constructed portfolio are presented below

The recommended portfolio does not necessarily require shot selling. Short selling is a strategy used by traders and portfolio managers to speculate portfolio and investment so as to decide whether to sell or hold a portfolio. Short selling helps to hedge downside risks resulting from holding an asset or portfolio for a long period of time. In the case of the above portfolio and in line with the Kendall’s investment experience, it is not advisable to short sell since it is an optimal portfolio.

The 5-ETF portfolio that recommendable to invest in the case of Morgan is.

The net sector and geography exposure in the optimal portfolio identified for Kendall inQ2

The Geographical exposure of Kendall’s optimal portfolio identified in Question 2

If the investors allocates part of the portfolio to cash and Assuming the cash investment is the risk free rate and earn 3.75% p.a and there is no limit to borrowing and lending of the cash.

1.3 Conclusion

After the calculating the expected utility the two investors would choose only one ETF. This will be based on the optimal utility. The choice of one ETF will pose serious risk to any investor. Choice of one ETL exposes the investor to loss in case of future uncertainties. Moreover, if an ETF is chosen and it performs poorly, it will drain the capital of the investor. To reduce these risks, diversification is called for. To come up with an optimal risk portfolio the Markowitz Portfolio Theory was applied. Diversification of a portfolio implied that the portfolio created was spread through various sectors and a number of geographical areas. The geographical and sector concentration exposure of the portfolio shows the portions of the assets in different sectors and countries. In case of any sector or geography attached risk, it will not affect the whole portfolio. This reduces losses and retains the capital of the investors.

Bibliography

Bodie, Z., Kane, A. and Marcus, A. (2014). Investments. 10th ed. New York: McGraw-Hill Education.

Brinson, G., Hood, L. and Beebower, G. (1986). Determinants of Portfolio Performance. Financial Analysts Journal, 42(4)

Capaul, C., Rowley, I. and Sharpe, W. (1993). International Value and Growth Stock Returns. Financial Analysts Journal, 49(1)

Davidow, A. (2014). Fundamentally weighted indexing: Weighing the difference. [online] Charles Schwab & Co., Inc. Available at:http://www.schwab.com/public/file/P-6353249/Fundamentally_Weighted_Indexing_Weighing_the_Difference_retail.pdf [Accessed 06 Sep. 2019].

Malkiel, B. (2003). Passive Investment Strategies and Efficient Markets. European Financial Management, 9(1), pp.1-10.