Using newtons law force balance

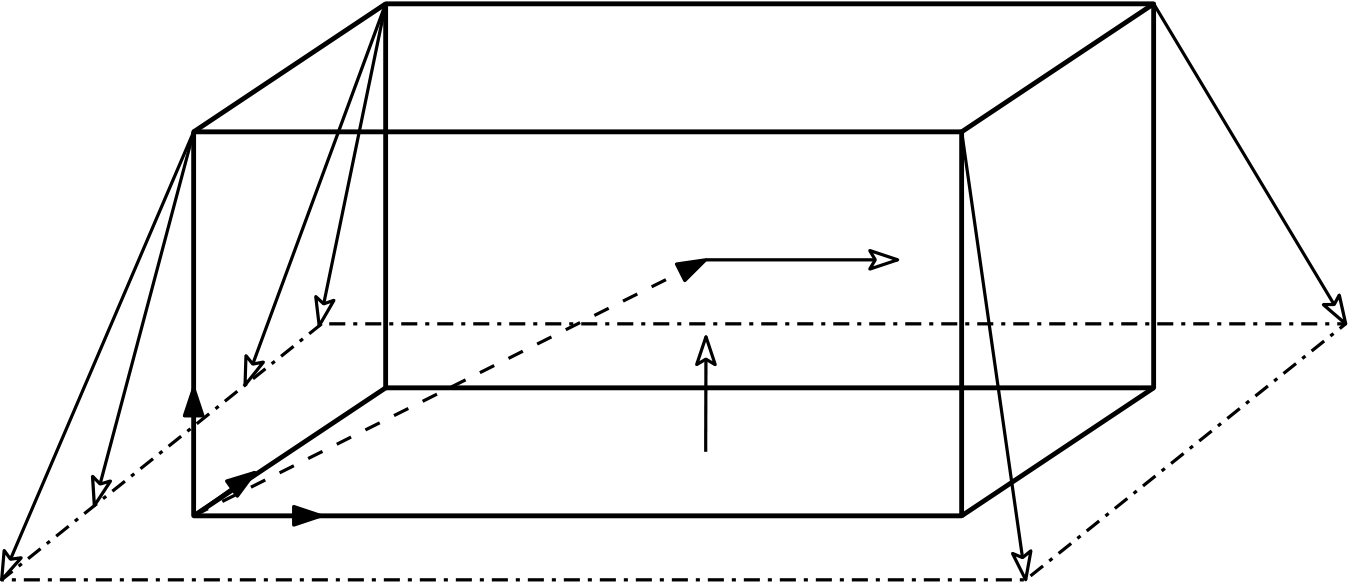
Cable Tension Problem

I = 50ˆi + 30ˆk
A = 30ˆk										G
K = 20ˆj + 30ˆk										G
F = −15ˆi + 40ˆj E = −15ˆi + 20ˆj B = −15ˆi − 20ˆj C = −15ˆi D = 25ˆi + 10ˆj + 15ˆk			A		T3	T4		D	9g		I	T5
			A		E			R	9g		I	T5
L = 25ˆi + 10ˆj	T1	C		T2			L
L = 25ˆi + 10ˆj	T1	C		Z			L
O					X
B					J
AC\|=√(−15)2+(−30)2 (−15ˆi−30ˆk), KE = ˆ Now, using Newton’s law of force balance, we have as follows. � F = 0 ⇒ 9gˆi + T1 ˆ AB + T2ˆ AC + T3ˆ KE + T4ˆ KF + T5ˆ GH + T6ˆ IJ + Rˆk = 0 which gives the three equations as follows along

� MK = 0 ⇒ � −→r × −→simplification gives as follows. F = 0 ⇒ −−→KA × T1ˆ AB +−−→KA × T2ˆ AC +−→KI × T6ˆ IJ +−−→KG × T5ˆ GH +−−→KD × 9gˆi +−−→KL × Rˆk = 0 which on

15.3644T1 + 17.8885T2 + 15.3644T6 − 10R = 0