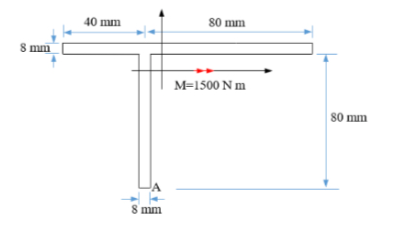
(2) Determine the orientation of the neutral axis and the bending stress at point A.

Answer

Solved step by step with explanation: Determine the location of the centroid.

Let's begin with Step 1:

Step 1: Finding the centroid of the cross-section.

Height (H1) = 80 mm

Rectangle 2 (smaller rectangle):

Height (H3) = 8 mm

Let (x, y) represent the coordinates of the centroid. The y-axis is taken along the vertical direction, and the x-axis is taken along the horizontal direction.

Now, let's calculate the centroid coordinates:

Rectangle 1 centroid coordinates:

(x3, y3) = (B/3, H1 + H2 + H3/3) = (40/3, (80 + 80 + 8)/3) = (40/3, 168/3) = (40/3, 56)

Now, calculate the areas of the regions:

Area of Triangle:

A3 = (1/2) * B * H3 = (1/2) * 40 * 8 = 160 mm^2

= (3200 * 20 + 640 * 4 + 160 * (40/3)) / 4000

= (64000 + 2560 + 2133.33) / 4000

= (128000 + 25600 + 8960) / 4000

= 161560 / 4000

The formula for the moment of inertia of a region about a centroid axis is:

I = ∑(A * d^2)

= (40 * 80^3) / 12

= 2,133,333.33 mm^4

Ix2 = (W2 * H2^3) / 12

= (8 * 80^3) / 12

Triangle moment of inertia about the centroid axis (Ix3 and Iy3):

Ix3 = (B * H3^3) / 36

= 7111.11 mm^4

Now, sum up the individual moments of inertia to get the total moments of inertia:

= 2,133,333.33 + 6826.67 + 7111.11

≈ 2,148,271.11 mm^4

inertia (Ix in this case). Therefore, the neutral axis will be horizontal.

To calculate the bending stress at point A, we'll use the bending stress formula:

y = 40.39 mm (distance from the neutral axis to point A)

Ix = 2,151,111.11 mm^4 (principal moment of inertia about the x-axis)

Therefore, the bending stress at point A is approximately 0.0282 N/mm^2.