Treesfigure tree imbalance and rotations avl trees
9
Trees
Trees, when used well, are a useful data structure for the storage and retrieval of data in a program. Trees represent a different type of data structure to what we have studied in the unit so far – so far all of our data has stored in a linear format, e.g., an array, a linked list, a stack, a queue, and so on. In this session we begin by introducing the concepts and terminology of trees in general, before undertaking a closer examination of binary trees and the Binary Search Tree in general. We examine the problem of imbalance which can affect the Binary Search Tree and discuss one of the known solutions to this problem, the AVL Tree. We finish the session with an examination of the heap data structure, which effectively overlays a tree structure onto an array to solve different problems, including the problem of the priority queue and sorting.b
9.2. General Concepts
| • | 57 | |
|---|---|---|
Session 9. Trees
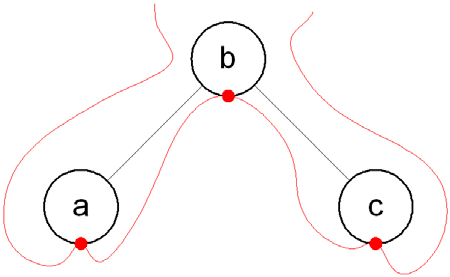
Figure 9.1: An Example of a Tree Data Structure
Given the above property of the binary tree, it is possible to calculate the range of the height of
| the tree ( | H |
|
|---|
| Binary Trees |
|---|
Figure 9.5: Breadth-First Traversal of a Binary Tree
Given the difficulty of navigating the tree to find all nodes for a particular level, a queue is used to simplify the task using the following algorithm:
|
|
|
|---|---|---|
Notice how each of the algorithms are recursive and that the only difference between the three traversals is the location of the call to process the current node (processNode(current)).
|
|||
|---|---|---|---|
| (a) | (b) | (c) |
Figure 9.6: Depth-First Traversals of a Binary Tree
 |
|---|
9.3.1. The Binary Search Tree
The Binary Search Tree (BST) is a binary tree with the following rules applied:
for the Binary Search we examined in Section 8.2.2, however unlike the Binary Search which requires an ordered/sorted array, the BST can be progressively constructed in the same way as a linked list, as we will see.
| 61 |
|---|
Session 9. Trees
From the rules presented above for the BST, if follow a reference to the left we will always find a lower value, thus, we can determine the minimum value stored in the BST trivially:
Algorithm 9.3: BST Maximum
To search for an item stored in the BST, we utilise the same rules, this time deciding whether to go left or right based on the value of the currently referenced node, as follows:
| Binary Trees |
|---|
Inserting a new value into a BST is a very similar algorithm. In particular, we search through the tree to find the correct location for the new value, however instead of terminating our search we attach the new node, as follows:
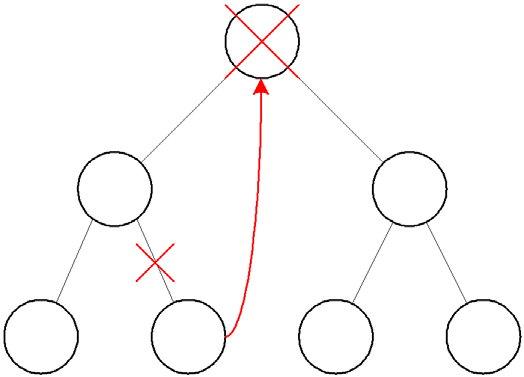
Deletion of a value from a BST is more complicated however. In particular we must consider three possibilities:
 |
|---|
• Deletion of a leaf node – this is straightforward, we just set the reference to the leaf to null to disconnect the node from the BST;
• Deletion of a node with a single outdegree branch/one child node – this is also relatively straightforward, the reference to the deleted node can just be replaced with a reference to the child of the deleted node;
•
Deletion of a node with two outdegree branches/two child nodes – this is much more complicated, each sub-tree of the deleted node could be many levels deep, and it isn’t possible to replace two references with one.The solution to the problem however is reasonably trivial, at least conceptually. In particular, if you consider carefully the ordering of values in a BST, we can see the following:
| Binary Trees |
|---|
The algorithm for deleting a node from a BST is presented below using recursion for simplicity. It is also possible to write an equivalent iterative algorithm, however this would be longer and less clear
|
O | log2n | | . However, consider constructing a BST |
|---|
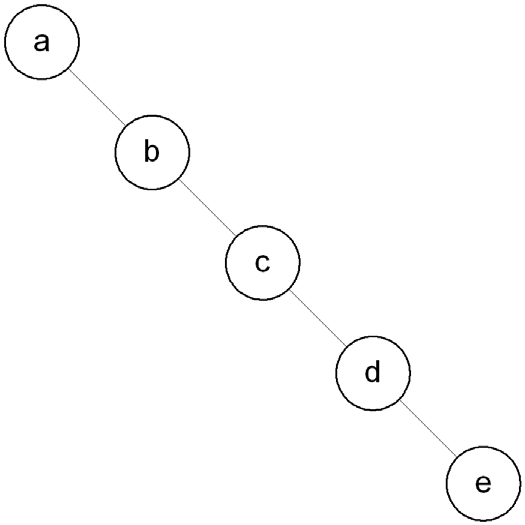
from the input data {a, b, c, d, e}, which would result in the BST illustrated in Figure 9.9.
 |
|---|
The same input data would result in the AVL tree illustrated in Figure 9.10, a nearly-complete BST.
| B | = | H left |
|---|
The tree balance is then maintained during insertion and deletion operations through the application of rotations to four different problems. To understand these rotations, we must first define the following:
• A tree/sub-tree is left-high when H leftH right
Figure 9.10: AVL Tree Correcting BST Imbalance
|
Binary Trees |
|---|
• All descendent nodes have a value that is less than or equal to the root node; and• Each sub-tree is also a heap.
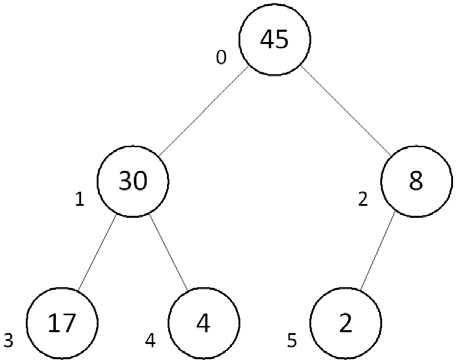
The heap also has the property that it is always either complete or nearly complete, an example of which is illustrated in Figure 9.12.
 |
|---|
| related nodes, both parent nodes ( | P | ) and child nodes ( | C | ), where represents the index of a |
|---|
node being referenced:
To allocate an array to store a heap, it is important to first calculate the correct size for the array. For example, if a request is received to create a heap of size 10, an array should be allocated to store 15 elements, due to the structure of a tree:
| size | = | 2 |  |
log2n |  |
|---|
| Binary Trees |
|---|
last node stored in the array, then rearranging the data stored in the array to reestablish the heap. This is divided into two methods for clarity, as follows:
|
O | log2n | | ); |
|---|
2. The value from the last used element in the array replaces the root node each time. However if instead the value of the root and last used nodes are swapped, the deletion algorithm transforms into another sorting algorithm known as the heap sort. The heap
| 69 | |
Task 9.1. Binary Search Tree
Objective: The Binary Search Tree implements many of the concepts that are important to understanding trees in an example that is easy to understand and, when balanced, performs well. In this task we examine the implementation of the Set data structure using a Binary Search Tree implementation.
3. Write a Main method that tests your Set by creating a set of integers and allowing the user to add or remove as they wish. Notes:
• The program must display relevant error messages if a duplicate is stored, etc., not crash;
• Use the CopyTo() method of your set class to retrieve the values stored in the tree and display them on the screen after each step;
• Also display the current, minimum, and maximum heights after each step.