Theorem and bayesian inferencebayes theorem

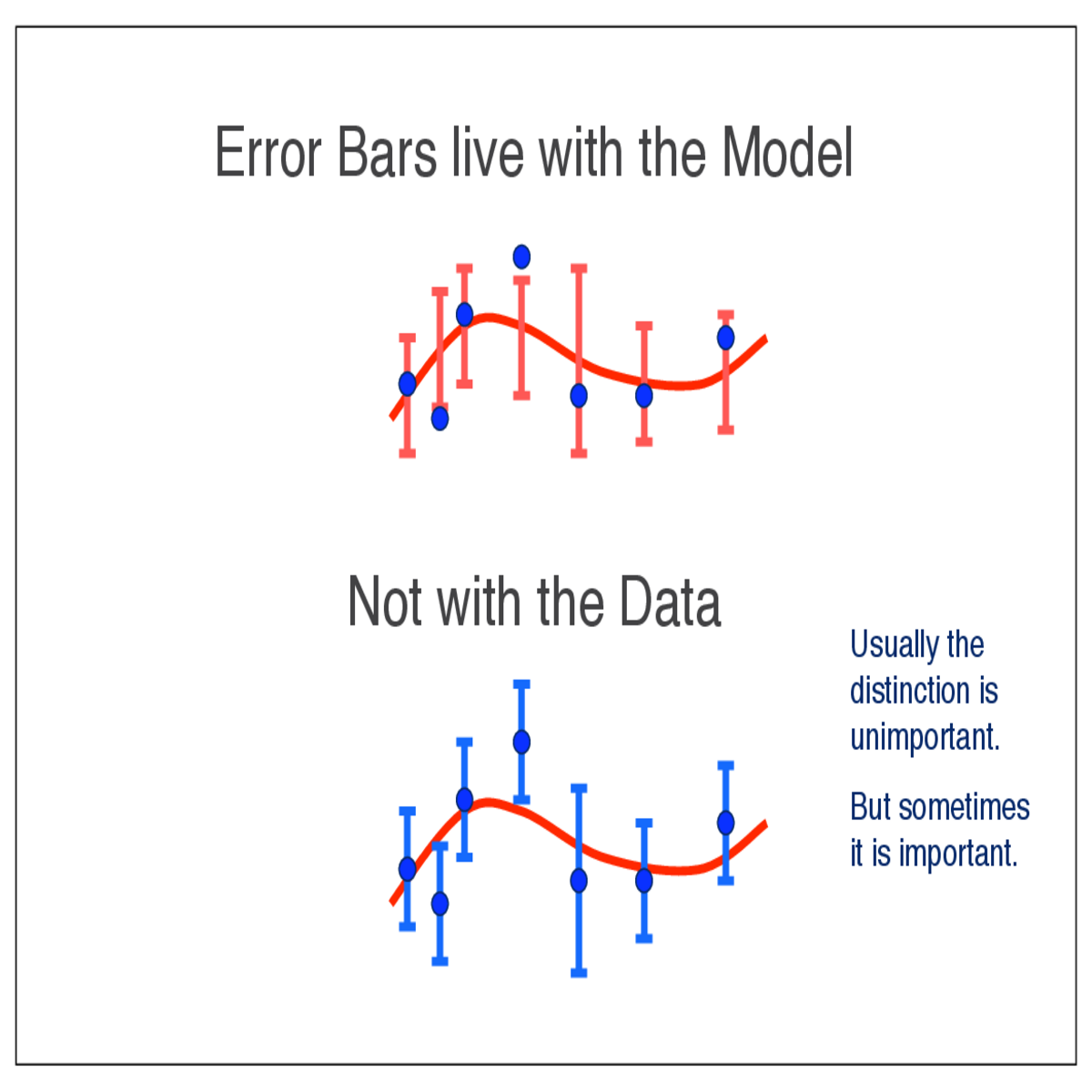
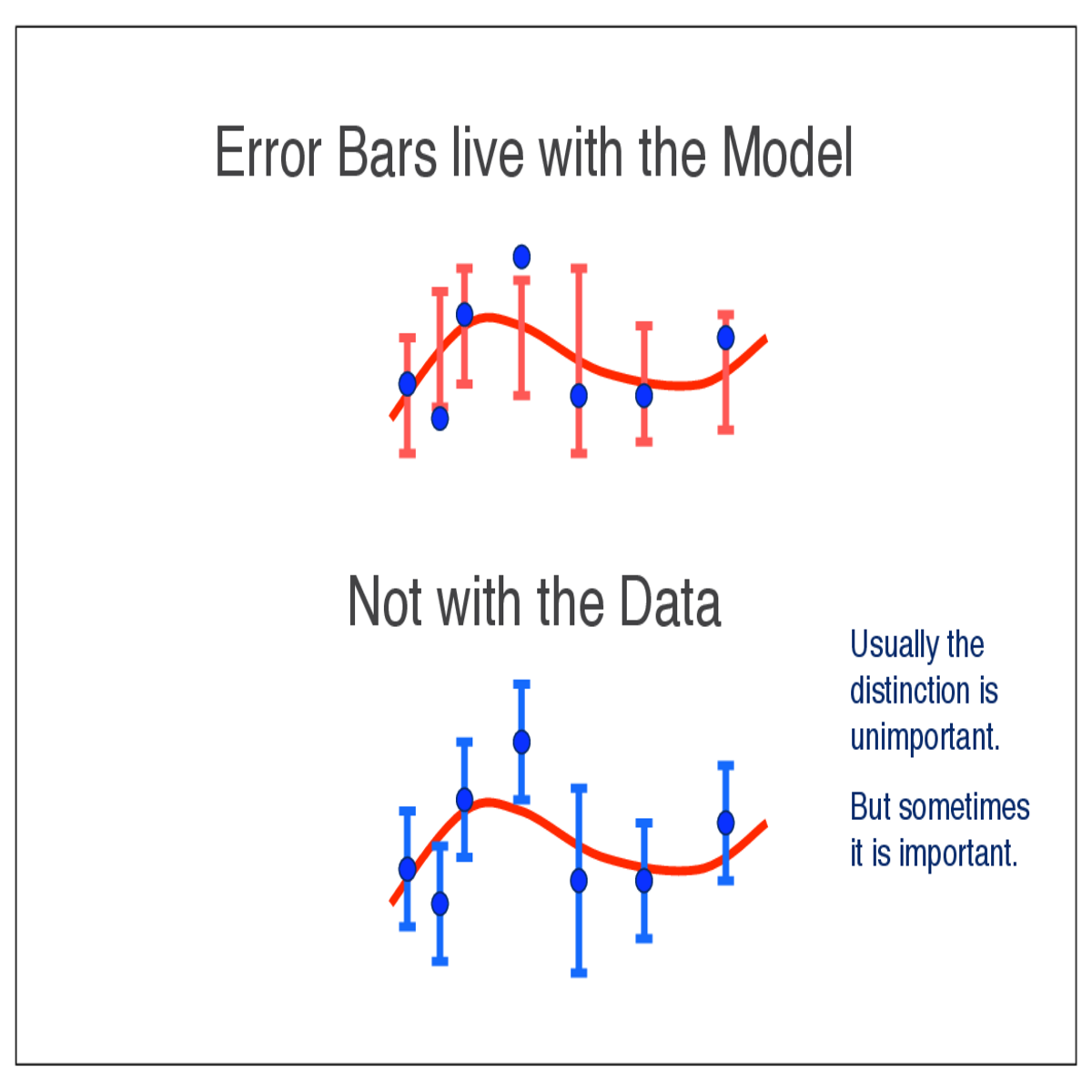
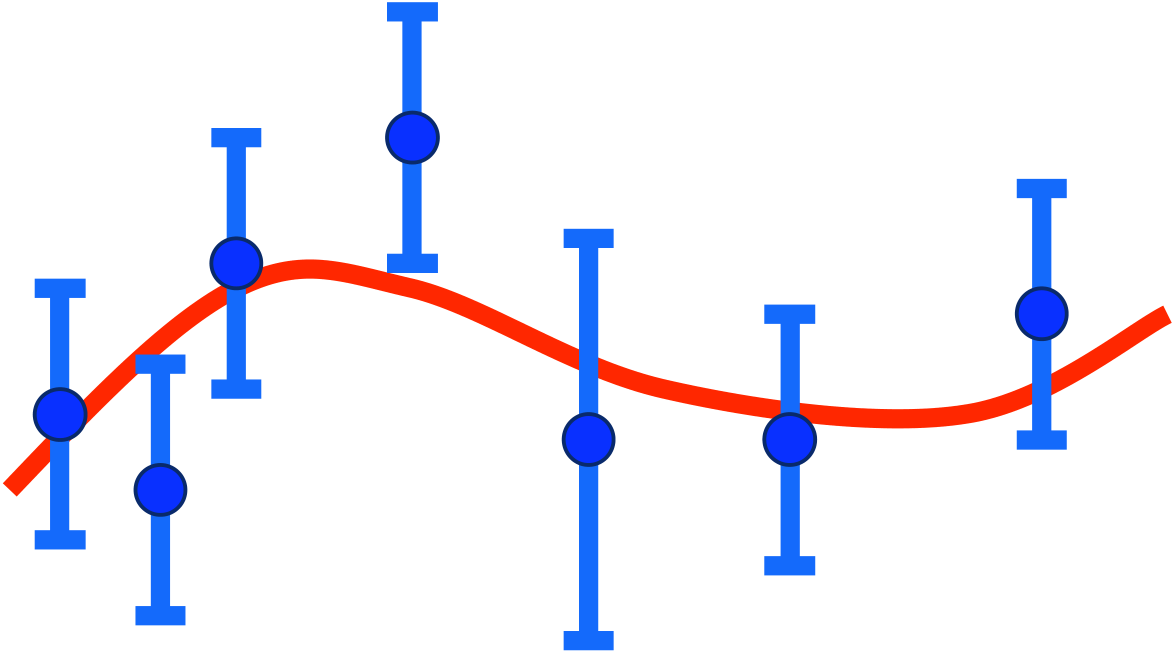
Error bars live with the model, not the data!

Example: Poisson data:	n = 0, 1, 2, ...
					8
					6


Xi = �, �2(Xi) = �				0		5
How to attach error bars to the data points?
The wrong way:	) =		Xi, then 1 �2= � when Xi = 0
and ˆ X �
and ˆ X �		i�

Assigning σ(Xi )= √ Xi gives a downward bias. Points lower than average by chance are given smaller error bars, and hence more weight than they deserve.

The right way:�

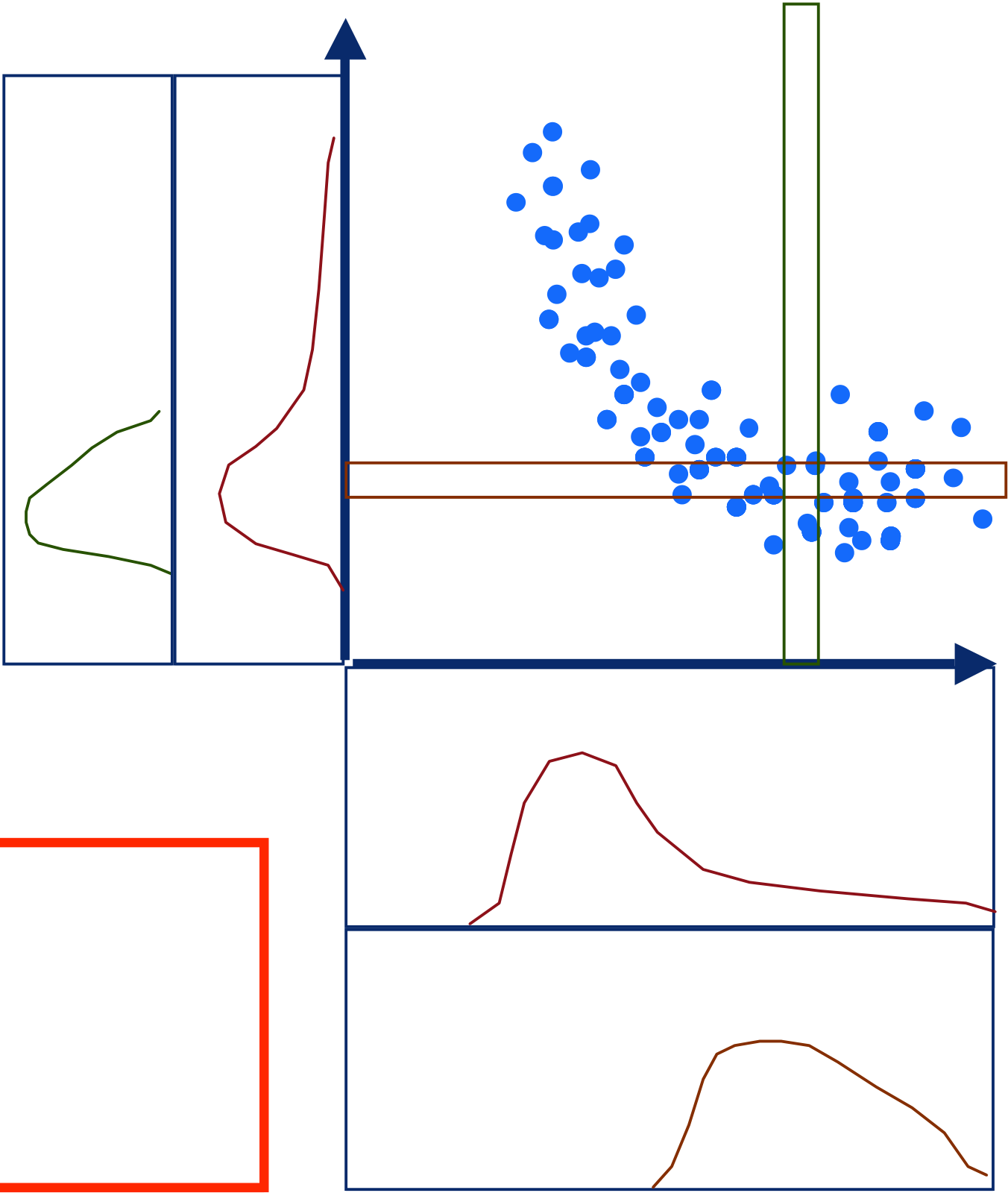
P( Y | X = 2 ) = ?

6 Y

Y = 3 X
X = Gaussian

1 2 3 X

Uniform P( log α ) P( α ) ~ 1 / α

• Different priors P(α) lead to different inferences P( α \| X )

�2	Parameter Space	Model	X2

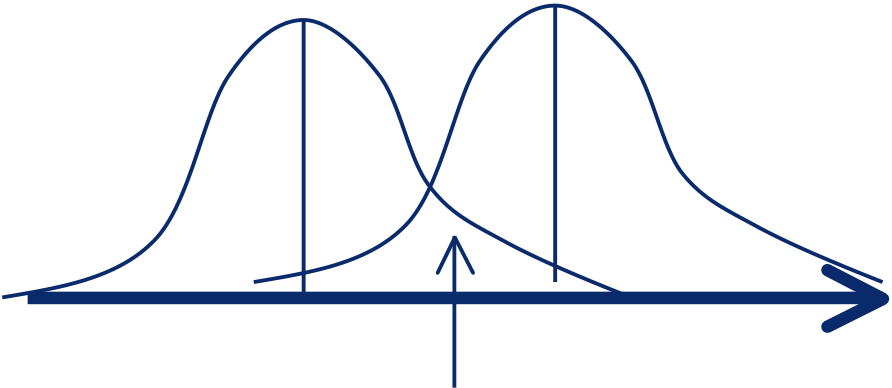
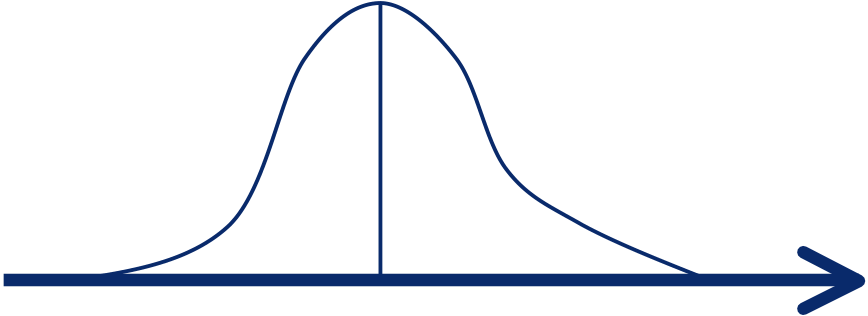
Gaussian Datum with Gaussian Prior

Likelihood : L(µ) = P(X |µ)

� � �

� 2

�

µ�µ0� � � 0

Likelihood:�

P(µ)
�

� �

�2 + 1� 0

2

Gaussian Data with Gaussian Prior

(2�)

N / 2

i�� i

(2�)

N / 2

i�� i

�

2� �

�1

2
�

2�

= e

�1 2

� µ�µ ML

�

� �

µML =

� 0

i�

� i

�2µML

) =

i�

� i

+	� 0

� i

point.�

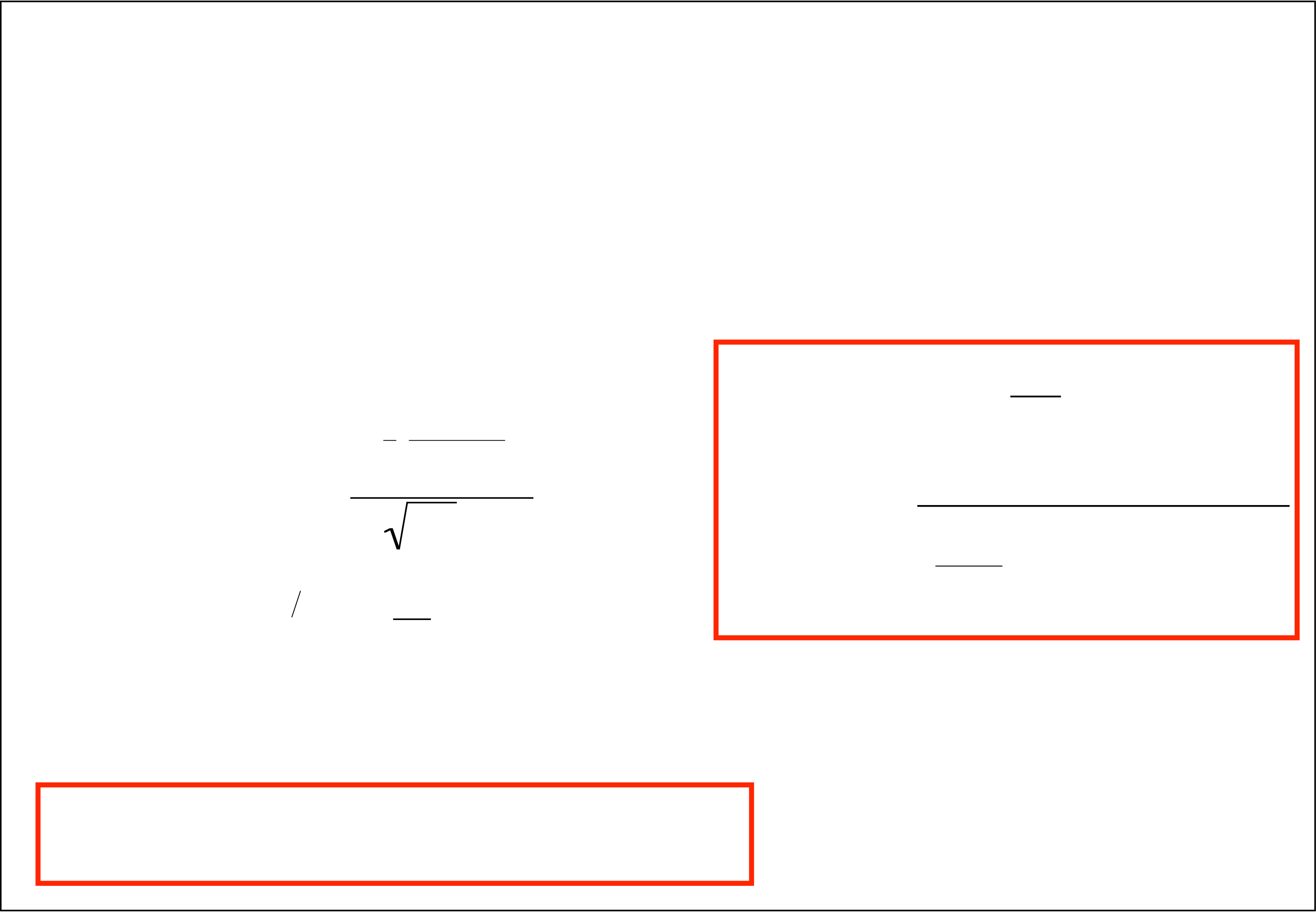
Max Likelihood for Gaussian Data Likelihood of parameters α for a given dataset:

�	N
	�
	�
	i=1

For Gaussian error distributions:

P(Xi \|�)

				2� � i
	� i=1		1		� �N / 2
	� i=1		� i		� �N / 2
�2 lnL = �2+ 2		ln� i + N ln 2�

Var[�ML] � � �2 �

� To maximise L(�), minimise �2+ 2 i�

	i	20
		18




		10
		8

Poisson data X with rate parameter λ :												4		2	4	6	8	Xi	10
Poisson data X with rate parameter λ :												2
												0
												0
												0.3		λ=1
Likelihood for N Poisson data points :												0.25
												0.25				λML=4.5�
												0.2
�	L(�) =		N		P(Xi \| �)			=		N		0.2
												0.15
																λ=7
			�							�
												0.1
												0.1
			i=1							i=1		0.05		�		6	8		10
lnL =		i�		( � � + Xi ln� � ln Xi!								0.05
												0
												0		2	4
Maximum likelihood estimator of λ :												1.2	0	2 �	4	�
Maximum likelihood estimator of λ :												1
							i�		Xi			1
												0.8
												0.6
												0.4
												0.2
																6	8	10
�						i�		Xi			.
												0
												-0.2
												-0.2				�