Then find the relation between and log log and log log log log log log log log

		NUMBER SYSTEM

3 (c)Proper fraction : Numerator < Denominator i.e. 5 5 (d)Improper fraction : Numerator > Denominator i.e. 3 (e)Mixed fraction : Consists of integral as well as fractional part i.e. 7 32
5
•
(v)
as non-terminating type of decimal numbers e.g.	2,	3	4 2,	+	,3	2	+	3,	4 7	3	etc.
(vi)
(vii)

Ex. Sol.	(viii)
	•	1 is neither prime nor composite number.


	(x)	Imaginary numbers: All the numbers whose square is negative are called imaginary

		Complex numbers: The combined form of real and imaginary numbers is known as complex numbers. It is denoted by Z = A + iB where A is real part and B is imaginary of Z and A, B ∈ R.

Square roots: the square root of a number x is that number which when multiplied by itself gives x as the

product. As say square of 3 is 9, then we can also say that a square root 9 is 3.

(i)It the unit digit of a number is 2, 3, 7 or 8, then it does not have a square root in N.

(ii)If a number ends in an odd number of zeros, then it does not have a square root in N.

Pg - 2

CUBES AND CUBE ROOT:
Cube: If any number is multiplied by itself three times then the result is called the cube of that number.

Hence, we must multiple 675 by 5 so that the product becomes a perfect cube.

SURDS AND EXPONENTS (INDICES):

rational. Also the symbol n		is called the radical sign and the indeed n is called order of the surd. na is

Similar examples		3	5, 12, 7, 12
(ii)2 + √3 is a surd (as surd + rational number will give a surd)
(iii)	Similar examples 3− 2, 3 + ,1 3 3 + 1,......			3)

Similar example																			7			+		4 3, 9						−	4 5, 9		+
(iv)33 is a surd as															3				3		=			3	1				3	1	=		Similar example			3 3		5,		6	,…..
(iv)33 is a surd as															3				3		=			3	2				3	6	=	6	Similar example			3 3		5,	4 5	6	,…..		3	12, 36	>	5	25

										3		8 =					3		2		3	which is a rational number.
(B)	2 +			3,			because									2 +						3
(C)3				3
Laws of Surds:					( n		a		) n		=			n		a		n		=
i.					( n		a		) n		=			n		a		n		=
ii.				n			a	×		n		b		=			n		ab									[Here order should be same]
iii.				n			a		÷	n		b			=			n
iii.				n			a		÷	n		b			=			n
iv.				n m				a		=		nm				a			=		m n
v.				n			a		=×n p					a
Or,				n			a	m		=		n p					a		m p									[important for changing order of surds]
Ex. Sol.
Ex.	Simplify:							8 ab 2							×		3		4		a b 2
Sol.	6	8	315 ab			3	×		6	4		2	a b 4					4	=			4	a b 3			6	2
Ex.	Divide:						24 by 3200
Sol.	3	24		=			6									=			6			216
Sol.	3	200		=			6	( 200					) 2			=			6			625

																																		n	x >		n	y	e.g.	3	16	>

and so on.

Pg - 4

2 = 2 6 2 6 = 12 64

3 3 = 3 4 3 4 = 12 81

Conjugate Surds:

Pg - 5

(ii)
(i) Common logarithm: in this system base is always taken as 10. (ii) Natural logarithm: in this system the base of the logarithm is taken as ‘e’, where ‘e’ is an
	If log3a = 4, find value of a. log3a = 4
Sol.			9	27÷ 32					3 + log 4
Sol.			8	27÷ 32					3 + log 4
= log					9	×	27			×	3
= log					8		32				4
= log1 = 0
Ex. Sol.	If 2 log4x = 1 + log4(x – 1), find the value of x. Given: 2log4x = 1 + log4(x – 1) log4x2 – log4(x – 1) = 1

FACTORS AND MULTIPLES:
Factors: ‘a’ is a factor of ‘b’ if there exists a relation such that a × n = b, where ‘n’ is any natural number. ❖1 is a factor of all numbers as 1 × b = b.

For examples, 36= 22× 32. 36 is expressed in the factorized from in terms of its basic prime factors.

Number of factors : for any composite number C, which can be expressed as C = ap× bq× cr× ……, where a, b, c.. are all prime factors and p, q, r are positive integers, then the number of factors is equal to (p + 1) × (q + 1) × (r + 1) ….. e.g. 36 = 22× 32. So the factors of 36 = (2 + 1) × (2 + 1) = 3 × 3 = 9.

So, the total number of odd factors is (7 + 1)(2 + 1) = 24.

Therefore, the number of even factors = 168 – 24 = 144.

There are one thousand lockers and one thousand students in a school. The principal asks the first student to go to each locker and open it. Then he asks the second student go to every second locker and close it. The third student goes to each locker and opens it. The third student goes to every third locker, and if it is closed, he opens it, and it is open, he closes it. The fourth student does it to every fourth locker and so on. The process is completed with all the thousand students.

(i)How many lockers are closed at the end of the process?

How many times a locker will be accessed depends on the locker no. if it contains odd number of factors, then it will be open and if it contains even number of factors. Then it will be closed. We know that a perfect square contains odd number of factors while a non-perfect square contains even number of factors. Thus the lockers with perfect square number will be open and the number of these perfect squares form 1 to 1000 determines the no. of open lockers.

(i)No. of closed lockers = No. of non-perfect square numbers from 1 to 1000 = 1000 – 31 = 969. (ii)Upto 500 students they can go to two or more than two lockers, while the rest 500 can go to only one locker.

HCF (highest common factor): The HCF of given numbers, as the name suggests is the largest factor of the given set of numbers.

Consider the numbers 12, 20 and 30. The factors and the multiple are

Ex. Sol.
	We should have the maximum number of students in a class. So we have to find HCF (437, 342) = 19. HCF is also the factor of difference of the number. Number of classes = 437 + 342 = 23 + 18 = 41 classes. 19 19
HCF of fractions = HCF of numerators HCf of denominators
Ex. Sol.
Ex. Sol.	(ii) How many times will they toll together in 30 min? The time after which all six bells will toll together must be multiple of 2, 4, 6, 8, 10 and 12. Therefore, required time = LCM of time intervals.
		 
1 is added as all the bells are tolling together at the start also, i.e. 0th second.
Ex. Sol.	LCM of two distinct natural number is 211. What is their HCF?
Ex. Sol.

DIVISIBILITY:
Division Algorithm: General representation of result is, Dividend = (Divisor × Quotient) + Remainder

No.	Divisibility test
2
3	The sum of digits of no. should be divisible by 3
4	The no formed by last 2 digits of given no. should be divisible by 4.
5
6
8
9
11	The difference between sums of the digits at even & at odd places should be zero or multiple of 11.
25	Last 2 digits of the number should be 00, 25, 50 or 75.


= 36		k2 1 + 48k1 + 16 + 36	k + 60k2 + 25 2
= 36 k2 1 + 48k1 + 36 k + 60k2 + 41 2
Ex. Sol.	37 37 259 is divisible by 37, When 139 divided by 37, leaves a remainder of 28.
Ex. Sol.	A number being successively divide by 3, 5 and 8 leaves remainders 1, 4, and 7 respectively. Find the respective remainders if the order divisors be reversed.

(i) Binomial expansion :

(a b) n = a n + 1!a n n 1-b n(n -1)

a n-2 b 2−....... ( + − n )1 b n

Hence, first term is pure of a i.e. an and last digit is pure of b, i.e. bn

Since, in 21 unit digit is 2, in 22 unit digit is 4, 23 unit is 8, in 24 unit digit is 6, after that the unit’s digit repeats. e.g. unit digit (12)12 is equal to the unit digit of, 24 i.e. 6.

(ii)When there is 3 in unit’s place of any number.

(vi)When there is 7 in unit’s place of any number.

(ix)When there is zero in unit’s place of any number. There will always be zero in unit’s place.


(a b) n = a n + 1!a n n 1-b n(n -1) 2! Sol. 31786 = (30 + 1)786 = 30786 + 786 × 30785× 1 + 786(786−)1× 30784× 12 + ……+ 1786. !2
Ex. Sol. Ex. Sol.	Find the last two digits of 7156747. last two digits will be 91(7× 7 gives 9 and 1 as units digit) Find the last two digits of 51456× 61567.
Ex. Sol.	(iii) Last two digits of numbers ending in 2, 4, 6 or 8: There is only one even two-digit number which always ends in itself (last two digits) – 76 i.e. 76 raised to any power gives the last two digits as 76. Therefore, our purpose is to get 76 as last two digits for even numbers. We know that 242 ends in 76 and 210 ends in 24. Also, 24 raised to an even power always ends with 76 and 24 raised to an odd power always ends with 24. Therefore, 2434 will end in 76 and 2453 will end in 24.
Ex. Sol.

		y		+ 	y			+ 	y			……, where [ ]
		x			x	2			x	3	


		20 = 5. 22

Hence, 5 numbers contribute an extra 1 to exponents. Similarly, there are 2 numbers that are divisible by 23 and 1 number that is divisible by 24. Hence, the total 1s contributed to the exponent of 2 in 20! Is the sum of (10 + 5 + 2 + 1) = 18. Hence, group of all 2s in 20! Gives 218× (N), where N is not divisible by 2.

Binary system has 2 digits: 0, 1
Octal system has 8 digits: 0, 2, …., 7
Hexadecimal system has 16 digits: 0, 1, 2,…., 9, A, B, C, D, E and F.

After 9, we use the letters to indicate digits. For instance, A has a value 10, B has a value 11, C has a value 12, …. So on in all base systems.

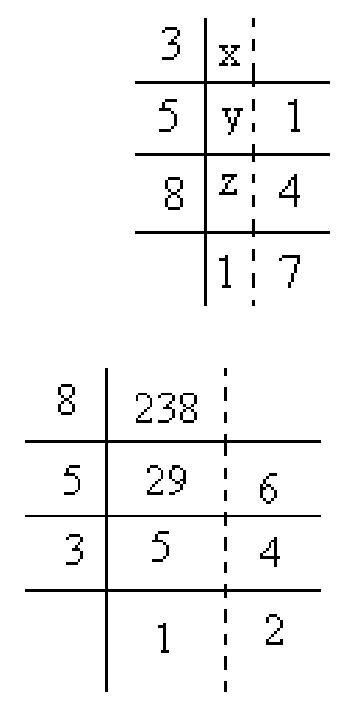
The number in decimal is consecutively divided by the number of the base to which we are converting

1 = 80× 1

(231)8 = (153)10

13.461 + 462 + 463 + 464 is divisible by : a) 3 b) 10	c) 11	d) 13

a) 12 b) 24 c) 12 – x

d) Multiple of 12


16.Find the unit digit of (795 – 358). a) 6 b) 4	c) 3
17.When a number P is divided by 4 it leaves remainder 3. If the twice of the number P is divided by the same divisor 4 than what will be the remainder?
a) A b) 5 c) 1		d) None of these

a) 1 b) 2 c) 3		d) None of these
22.What is the remainder when 763 divided by 344? a) 1 b) 343
		d) 0
24.A number when divided successively by 4 and 5 leaves remainders 1 and 4 respectively. When it is successively divided by 5 and 4, then the respective remainders will be: a) 1, 2 b) 2, 3 c) 3, 2 d) 4, 1 b) 2000 c) 1922 d) None of these a) 1936

a) 2000 b) 1936 c) 1849 d) None of these

30.In the case of previous question, how many rooms will be closed in all?

once?

a)32 b) 34 c) 35 d) 36

a) 9000 b) 4536 c) 4464 d) None of these

35.Find the total number of prime factors in the expression (4)11× (7)5× (11)2.

divisible, is :

a) 6 b) 24 c) 48 d) 96

smallest original number is :

a) 12 b) 22 c) 26 d) 53

the remainder. The number is :

a) 1220 b) 1250 c) 22030 d) 220030

43.Anita had to do a multiplication. Instead of taking 35 as one of the multipliers, she took 53. As a result,

the product went up by 540. What is the new product?

a) 1050	b) 540
noticed a bowl of mints at the front counter. Sita took 1/3 of the mints, but returned four because she had a monetary pang of guilt. Fatima then took ¼ of what was left but returned three for similar reasons. Eswari the decimal number system, becomes: a) 406 b) 1086 c) 213 d) 691
47.What is the value of the following expression ( 2		1		1 )	  +		( 4		1				( 6	1			...	+			1			?
47.What is the value of the following expression ( 2		2	−	1 )	 		( 4		2	−	1 )		( 6	2	−	1 )				( 20	2	−	1 )	?
a) 9/19	b) 10/19
48.Consider a sequence of seven consecutive integers. The average of the first five integers is n. the average of all the seven integers is : a) n b) n + 1
		d) n +					 	2
		d) n +					 	7
49.Let N = 553 + 173 – 723. N is divisible by: a) both 7 and 13 b) both 3 and 13		c) both 17 and 7
a) 1182 b) 1912 c) 1192												d) 1292
the two number: a) 36 and 18 b) 78 and 60 c) 63 and 81 d) 52 and 34 a) 40 b) 37 c) 39 d) 38 55.In a certain examination paper, there are n question. For j = 1, 2, … n, there are 2n-j students who