The voltage across the the final voltageacross the
| 1270 |
|
||
|---|---|---|---|
| S 11 | |||
| EX: | |||
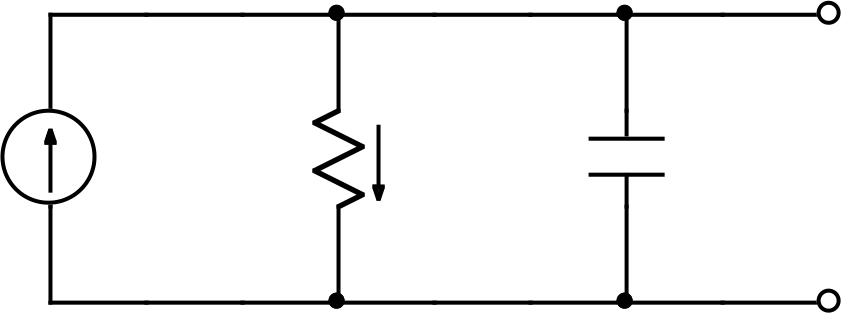
SOL'N: a) The following general form of solution applies to any RC circuit with a
single capacitor:
| � |
|---|
For time t = 0–, the current source will be off and the capacitor will have
| � |
|---|
flow through the resistor, resulting in a voltage across the resistor (and
capacitor) of igR.
b) The following general form of solution applies to any current in any RC circuit with a single capacitor:
i(t ≥ 0) = i(t → ∞) + [i(t = 0+) − i(t → ∞)]e−t /RThC
In the present case, this applies to the resistor current:� iR(t ≥ 0) = iR(t → ∞) + [iR(t = 0+) − iR(t → ∞)]e−t /RThC We have the same Thevenin resistance and time constant as before:
| � |
|---|
iR(t → ∞) = 30 V /2 kΩ =15 mA
Substituting values, we have the following result:
� iR(t ≥ 0) =15 mA + [0 −15 mA]e−t /1µs=15 mA−15 mA⋅ e−t /1µs
�





