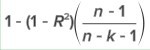The the following simple linear regression model
lOMoARcPSD|16107334

Saturday, April 20, 201912:37 PM
| quizlet we specify the alternative hypothesis as ha:p<0 when we want | to test if Two variables are negatively linearly related |
|---|---|
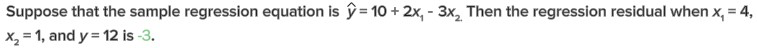 |
|
|
|
 |
|
| ables have that | |
| Which of the following statements is true about the test of Ho : Pxy = | 0?The test statistic is assumed to follow the tdf distribution with n-2 de freedom. |
| estimated. The ls 100, and for which model |
|
|
|
| If two variables X1 and Y1 have a covariance of 25 and two other varia have a covariance of 65, what conclusion can we draw about the relati | |
| When testing whether the correlation coefcient difers from zero, the test statistic is t20=1.95 with a corresponding p-value of 0.0653. At th level, can you conclude that the correlation coefcient difers from zer | value of the No, since the p-value exceeds 0.05. e 5%
signifcance o? |
|
|
STATS Page 1 |
|
lOMoARcPSD|16107334
|
|
|---|---|
|
|
| o judge the To avoid the risk of using the wrong model. | |
|
|
|
|
|
|
|
n between X Closet to -1 or 1 |
| Which of the following is NOT true of the standard error of the estimat | e?It can take on negative values |
|
|
|
|
|
ses, the other |
| The set of values of a test statistic for which the null hypothesis is rej | |
|
|
| How many explanatory variables does a simple linear regression mode |
|
| resents a pair | |
| The goodness-of-ft measure that quantifes the proportion of the varia response variable that is explained by the sample regression equation | |
|
|
|
|
|
|
|
|
| use certain variables that impact the response variable are not included i | |
|
|
| ses, the other | |
|
|
|
|
STATS Page 3 |
|
lOMoARcPSD|16107334 |
|
|---|---|
|
|
|
|
|
|
|
|
| mple linear | |
|
|
| T/F: In multiple linear regression for the sample regression equation, bi change in the predicted value of the response variable y(hat) given a u the associated explanatory variable xi, holding all other explanatory va | measures the True; bi represents the partial influence of xi on
y(hat)u nit increase in riables constant |
|
|
| Why do we use the multiple regression model instead of the simple re | gression model? We add explanatory variables to increase model's use |
|
|
|
|
|
|
|
|
STATS Page 5 |
|

| e on a straight | |
| e on a straight | |
| Calculate value of R2 given the ANOVA portion of the regression outpu | tR2=SSR/SST |
| Which of the following is not true of the standard error of the estimate | ?It can take on negative values. |
|
the variability of the observed y-values around the predicted y-value |
|
|
| Percent variability of y that is explained by the variability of x1 and x | |
| a simple linear Indicates whether the slope of the regression line is positive or negat | |
at would determination. |
|
|
|
|
variables and R2=1-SSE/SST |
| In the estimation of a multiple regression model with four explanatory 25 observations, SSE=660 and SST=1000 . The value of adjusted R2 is | |
| Consider the following simple linear regression model: y=Bo+B1X+Ę . determining whether x signifcantly infuences y, the null hypothesis ta | |
|
|
|
|
Since the p-value is 0.0028, which is less than α = 0.05, we can conc one explanatory variable is signifcantly related to the response varia |
|
|
he F2,20 test F(2,20)=MSR/MSE |
| The accompanying table shows the regression results when estimating signifcance level, which explanatory variable(s) is(are) individually sig | . At the 5% Since the p-values for the slope coefcients attached to x1 and x2 ar nifcant? signifcance level of 0.05, these two variables are both individually si |
| The accompanying table shows the regression results when estimating signifcance level, which explanatory variable(s) is(are) individually sig | |
used to study if
|
|
| In regression, the two types of interval estimates concerning y are call | ed: confidence interval and prediction interval. |
|
n the The prediction interval is for a particular value of y rather than for th |
|
|
|
|---|