The sum the torques the left ladder section must give zero
Chapter 3
Static Equilibrium
• The (vector) sum of the external forces on the rigid object must equal zero:
| � |
|
(3.1) |
|---|
| � | (3.2) |
|---|
When both 3.1 and 3.2 are satisfied we say that the object is in static equilibrium.
Nearly all of the problems we will solve in this chapter are two–dimensional problems (in the xy plane), and for these, Eqs. 3.1 and 3.2 reduce to
| � | � | � | (3.3) |
|---|
56 CHAPTER 3. STATIC EQUILIBRIUM
3.1.2 Two Important Facts for Working Statics Problems
Strategy for solving problems in static equilibrium:
• Determine all the forces that are acting on the rigid body. They will come from the other objects with which the body is in contact (supports, walls, floors, weights resting on them) as well as gravity,
3.2.1 Examples of Rigid Objects in Static Equilibrium
1. The system in Fig. 3.1 is in equilibrium with the string in the center exactly horizontal. Find (a) tension T1, (b) tension T2, (c) tension T3 and (d) angle θ.
| 3.2. WORKED EXAMPLES | �� | � | 57 |
|---|
��
���� ����
Figure 3.1: System of masses and strings for Example 1.
| �� | ��� | ���� | �� | ||||
|---|---|---|---|---|---|---|---|
| ��� | ��� |
Figure 3.2: (a) Forces at the left junction of the strings. (b) Forces acting at the right junction of the strings.
Whoa! Four unknowns (T1, T2, T3 and θ) to solve for! How will we ever figure this out?
In this problem the algebra really isn’t so bad. From Eq. 3.5 we get
| T1 = |
|
|---|
and Eq. 3.7 as:
T3 cos θ = 50.0 N (3.9)
Now if we divide the left and right sides of 3.8 by the left and right sides of 3.9 we get:
| T3 = |
|---|
Summarizing, we have found:
| T1 = 48.8 N | T2 = 28.0 N | T3 = 57.3 N |
|
|---|
3.2. WORKED EXAMPLES 59
| �� | � |
|
�� |
|---|
| ��� |
|
��� |
|---|
Now, one way to solve the problem would be to let the direction of the hinge force be some angle θ as measured from some line of reference. In fact it will probably be easiest to let the x and y components of this force be the unknowns... I will call them Fh,x and Fh,y. In fact, parts (b) and (c) of the problem ask us for these components directly. We can always get the direction and magnitude later!
Now let’s write down some equations. First, the sum of the Fx’s must give zero. Note (from basic geometry) that the force of the cable is directed at 30◦below the horizontal.
−MgL 2 sin 45◦ − mgL sin 45◦ + TL sin 15◦ = 0
but we note that we can cancel the L out of this equation, leaving
| so that | T sin 15◦ | = |
|
|
|---|---|---|---|---|
| = | ||||
| = |
|
|||
�
| ���� | �� |
|
|
|---|---|---|---|
| ��� | |||
| Fh,y | = |
|
|---|---|---|
| = |
|
|
| = |
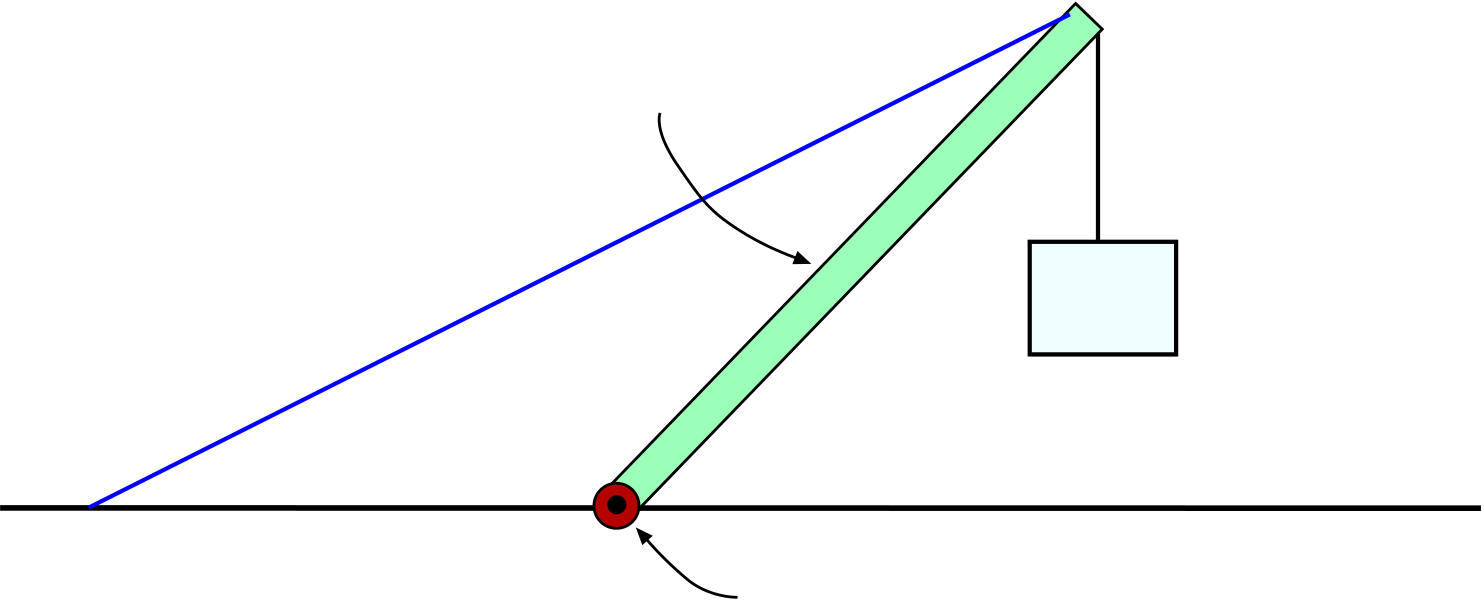
We make a basic diagram of the geometry of the problem in Fig. 3.5. The ladder has length L; we show the center of mass of the ladder at a distanceL 2up from its bottom end. If the student had climbed a fraction x of the ladder, then he/she is at a distance xL from its lower end, as shown.
Keeping the geometry in mind, we next think about all the separate forces that are acting on the ladder as it leans against the wall and supports the student.
��
�� ��
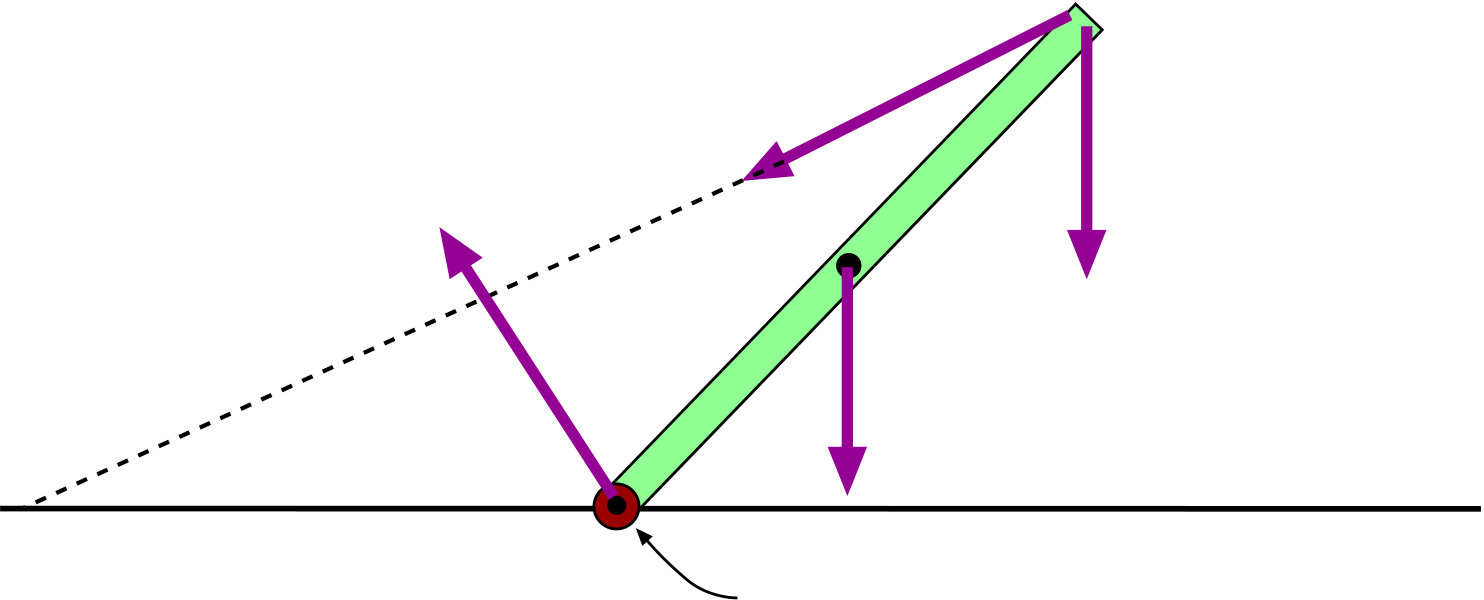
All these forces and their directions are diagrammed in Fig. 3.6. Now we apply the conditions for static equilibrium given in Eq. 3.3.
First off, the horizontal forces must sum to zero. That gives us:
|
(3.14) |
|---|
The next condition for equilibrium is that the sum of torques taken about any axis must give zero. Since we have two forces acting at the lower end of the ladder, it might be best to put the axis there because then those forces will give no torque, and we will have a simpler equation to deal with. We note that the gravity forces from the student and the ladder’s CM make an angle of 30◦with the line joining the axis to the application points; they give a clockwise (negative) torque. The normal force from the wall makes an angle of 60◦with the line from the axis, and it gives a positive torque. Our equation is:
| to get: | −xmg −mg 4 + | (3.15) |
|---|
We now have three equations, with four unknowns Nf, Nw, fs and x. (We can consider m as given. In fact, its value won’t matter.) We need another equation!
We have not yet used the condition that when the student is standing xL up from the ladder’s bottom it is just about to slip. Why should the ladder slip at all? It is because the force of static friction fs is limited in size; we know that it can only be as large as µsNf, since Nf is the normal force between the floor and the ladder’s lower end. When the student has walked up far enough that the ladder is on the verge of slipping then we have the equality
Put this result in Eq. 3.15 and we have:
−xmg −mg 4 +
| m): |
|
|---|
And at last, using the given value µs = 0.400:
| x = 3√ | 3(0.400) | |
|---|---|---|
Before anything else, we need to do a little geometry to find the angles which the ladder sides make with with floor, because we are given enough information for this in the problem.
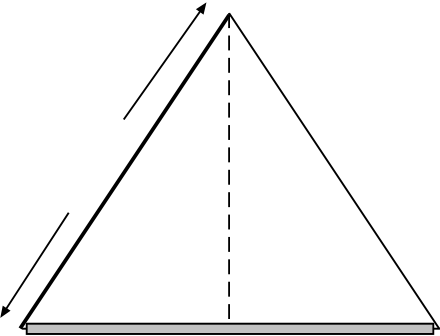
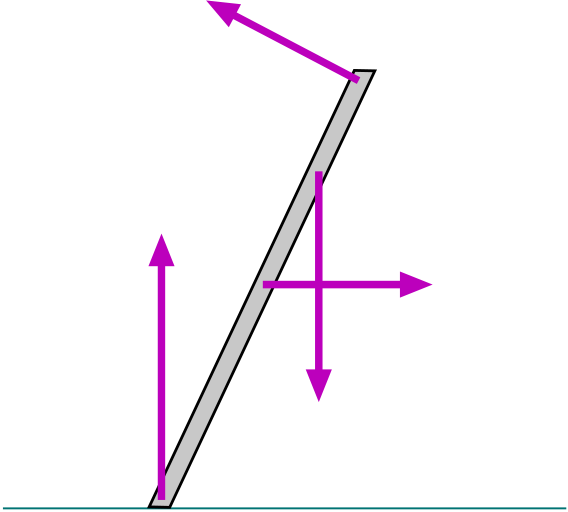
Figure 3.7: Man stands on a ladder in Example 4.
�
| � | �� | � |
|---|
| � | � | � | |||
|---|---|---|---|---|---|
 |
������� | ||||
Figure 3.8: (a) Some trigonometry to find the angle of slope of the ladder. (b) The forces which act on the left side of the ladder and their application points.

| cos θ = 1.25 4.00 = 0.3125 | =⇒ |
|---|
φ = 90◦− θ = 18.21◦
Now that the geometry is settled, we follow the hint and treat the sides of the ladder as separate objects for which we will apply the conditions of static equilibrium. First, consider the left side of the ladder (the one on which the man is standing). What forces are acting on it?
Fx + T = 0 (3.17)
The sum of the y forces on this part of the ladder gives zero:
66 CHAPTER 3. STATIC EQUILIBRIUM
��
zero:
−Fx − T = 0
But note that this equation is basically the same as Eq. 3.17. So we can
ignore it!
The sum of the y forces on this part of the ladder gives zero:
Here’s one way to go about solving this set of equations.
Notice that Fx only appears in 3.17, so we can wait until the very end to use it (if we want to get Fx). Combining 3.18 and 3.20 we get
| Fy = 192 lb − Nf | and |
|---|
T = 2N′fsin φ sin θ |
(3.23) |
|---|
−4(192 lb − N′f) sin φ + 2(0.658)N′fsin θ = −(192 lb) sin φ
Some more regrouping and evaluation of terms gives
Nf = 192 lb − N′f= 120 lb
|
|---|
| (a) | (b) | (c) |
|
|---|
But being the thorough kind of guy that I am, I’d like to find the components of the
68 CHAPTER 3. STATIC EQUILIBRIUM





