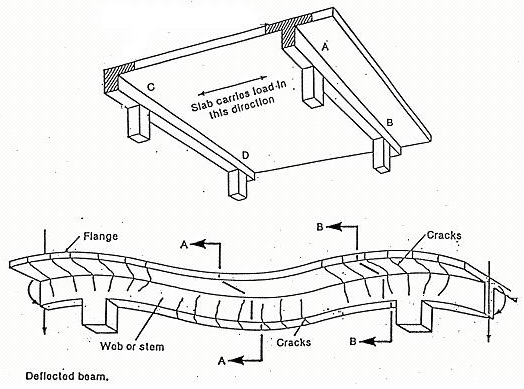
The stress block must extend below the flange

CE2003 Structural Mechanics / Structural Concrete Design 55

2.5

T-section

L-section

Section at span

	Section at support		Section at span

Actual
N.A.

Fig. 2.5-3 Stress blocks of T-beams. (a) Actual stress block; (b) equivalent stress block

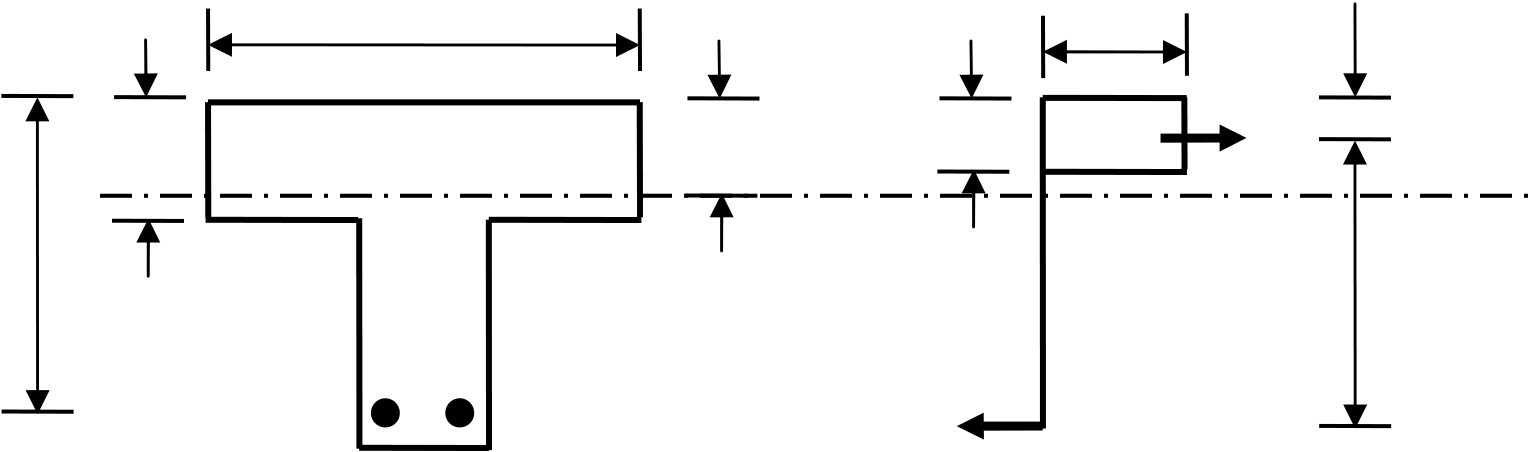
2.5.2Section with the depth of stress block lying within the flange(	s 	fh	)

CE2003 Structural Mechanics / Structural Concrete Design 57

bf	0.567fck
neutral axis	s = 0.8x	Fcc
As	Fst		z
	Stress block
Section	Stress block

	A s				M
where	A s				.0 87 f z yk			(2.10)
where	z		d[	5.0		.0 25		(2.9)
and	K M							(2.9)

2.5.3Analysis of a flanged section with the depth of stress block lying

within the flange(		s 

	.0567 f b s		.0 87 f			sx	z		d		s
From	ckf		.0 87 f	yk	s	or					2

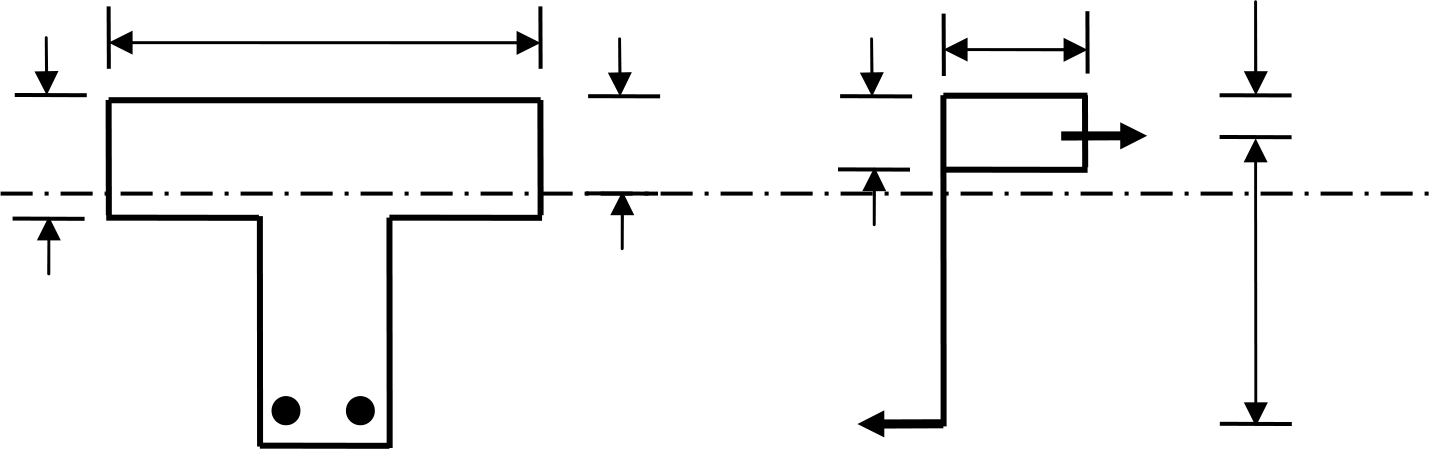
CE2003 Structural Mechanics / Structural Concrete Design 58

bf = 800	0.567fck		s/2
hf= 150 mm	s = 0.8x	Fcc	s/2
d=420 mm			z
As =1470 mm2
	Stress block
Section	Stress block

For equilibrium: Fcc = Fst
therefore

.0567 f b s ckf		.0 87 f	yk	A s

	s		.0 87
so			.0 567					25			
	x		56	mm 						fh		
	x		s /		8.0				70mm

CE2003 Structural Mechanics / Structural Concrete Design 59

x		.0 617d		.0 617			420		259
x		.0 617d		z					259

Taking moments about the centroid of As, the moment of resistance is

	F cc
	.0 567 f b sz ck f
	.0 567		25		800


check the depth of the stress block extends below the flange. An alternative

'
procedure is to calculate the moment of resistance, M , of the section with f
s fh , the depth of flange (see Fig. 2.5-4). Hence if the design moment, M , d

(b)designing for the conservative condition of	x .0 45d	, which is the

maximum value of x for a singly reinforced section and concrete class ≤

A Tsection (or Lsection) can be divided into flange component and web

component, as shown in Fig. 2.5-5.

bf	bf	bf	s/2=0.4x
As	Asf	Asw
As	Asf	Asw	z=d-0.4x
	bw
Actual section	Flange component
Actual section		moment M-Mf

Fig. 2.5-5 Flange and web components of a T-section

M	f		.0 567 f (b ck	f				5.0 h ) f	(2.29)

			M	f
sf		.0	87 f ( d yk		5.0 h ) f	(2.30)

oMoment of resistance of the web component

M	w		M		M		(2.31)

		A sw			M				M		
		A sw			.0 87 f z yk				.0 87 f z yk			(2.32)
where	z				.0 87 f z yk				.0 87 f z yk
where	z		d[	5.0			.0 25			K	w

								61
K			M		M			61
	w		b w	d f		ck

oTotal reinforcement area

A s		A sf		A sw	(2.33)

hf= 100 mm		0.567fck
hf= 100 mm		s = 0.8x
	As	N.A.
	As	Fst

M	'		.0 567			f	(	d		h	f
M	f		.0 567			f	(	d		h	f
	 0.567				25 400 100(350 - 100/2) 10								6
 170 kNm 180 kNm, the design moment

M	f		.0 567	f	ck	( b	f		b w	)	h	f	(	d		5.0	h	f

CE2003 Structural Mechanics / Structural Concrete Design 62

.0 56725 (400200) 100(3505.0100)

A		M
sf		.0 87 f ( d yk											651 mm2
sf		85					10		6				651 mm2
		.0 87		500(350					5.0		100 )

oFactor for the moment of resistance of the web component:

K			M				M							
	w		b w			d f		ck								
	w		(	180				85 ) 10					6			
z			200					350	2		25
		d[		5.0										K	w
		350			[	5.0			.0 25					.0 155 / .1 134 ]
		293 mm												.0 155 / .1 134 ]

A		M		M	f		(180		85 ) 10			6		745 mm
sw		.0 87 f z yk					.0 87		500		293

A s		A sf		A sw		651 745		1396 mm

Provide 3T25 (As = 1472 mm2).

(2) Design by the code method (EC 2)

		63
bf	0.567fck	63

x = 0.45d s = 0.8x

F c1				s				8.0		.0 45d

= 0.2fckbwd

F c2		.0 567 f ( b ck	f		b )h w

M		F st	(	d		5.0	h	f	)		F c 1		( / 2				5.0	h	f	)		h ) f
		F st	(	d	yks A ( d						F c 1		( / 2				5.0	h	f	)
		.087 f			yks A ( d					5.0		h ) f			1.0

A		M		1.0					h ) f
s							5.0 h ) f			(2.34)

Eq. (2.34) is only applicable when hf< 0.36d.

	CE2003 Structural Mechanics / Structural Concrete Design													64
	x 	.0 45d
oWith	x 	2
	M			F z c1 1		F z c2
			.0167 f b d ckw				2		.0 567 f (b ck	f			5.0 h ) f	(2.35)

Note: when using equation 2.34 to calculate the area of tension steel As, it is

necessary to confirm that the design ultimate moment should be	Mbal	in

M	'		.0 567			f	(	d		h	f	/ 2)
M	f		.0 567			f	(	d		h	f	/ 2)
Since					25 400 100(350 - 100/2) 10								
 170 kNm 180 kNm, the design moment

A		M		f1.0													h ) f
	s	.0 87f					yk	(d				5.0 h ) f													350		100)		1414mm
	180		10	6		1.0				25				200			350				( .0 36				350		100)		1414mm
	180	.0 87									500				(350				5.0				100)

2.5.5Flanged section with compression reinforcement

When the design ultimate moment

M	CE2003 Structural Mechanics / Structural Concrete Design													65
M		M	bal			2		.0 567 f (b ck	f					65

compression steel is required.

The moment (M – Mbal) will be resisted by compression steel. Hence,

M		M	bal		.0 87 f	yk	A ( d s		(2.36)

A	M		M	bal
s	.0 87 f ( d yk				d )

F st		F c1		F c2		F sc

0.87fykAs = compression of flange component + compression of web component + compression of steel A’s

	.0567 f (b ck		b )h w	f			8.0		.0 45d )		.0 87 f	yk

A s						b )h w		f
						.0 87 f
						.0 87 f
Again,	d'x		.0 38	or	d'd			.0 171	, otherwise the compression steel
										.087 fyk