The linear trend line equation isto calculate forecast for period

Forecasting

A forecast is a prediction of what will occur in the future. Meteorologists forecast the weather, sportscasters and gamblers predict the winners of football games, and companies attempt to predict how much of their product will be sold in the future. A forecast of product demand is the basis for most important planning decisions. Planning decisions regarding scheduling, inventory, production, facility layout and design, workforce, distribution, purchasing, and so on, are functions of customer demand. Long-range, strategic plans by top management are based on forecasts of the type of products consumers will demand in the future and the size and location of product markets.

In today's global business environment, strategic planning and design tend to focus on supply chain management and total quality management (TQM).

Supply Chain Management

Long-run forecasts of technology advances, new products, and changing markets are especially critical for the strategic design of a company's supply chain in the future. In today's global market if companies cannot effectively forecast what products will be demanded in the future and the products their competitors are likely to introduce, they will be unable to develop the production and service systems in time to compete. If companies do not forecast where newly emerging markets will be located and do not have the production and
distribution system available to enter these markets, they will lose to competitors who have been able to forecast accurately.

A recent trend in supply chain design is continuous replenishment, wherein continuous updating of data is shared between suppliers and customers. In this system customers are continuously being replenished, daily or even more by their suppliers based on actual sales.

An accurate forecast of customer traffic flow and product demand enables McDonald's to schedule enough servers, to stock enough food, and to schedule food production to provide high-quality service. An inaccurate forecast causes service to break down, resulting in poor

quality. For manufacturing operations, especially for suppliers, customers expect parts to be provided when demanded. Accurately forecasting customer demand is a crucial part of providing the high-quality service.

Components of Forecasting Demand

The type of forecasting method to use depends on several factors, including the time frame of the forecast (i.e., how far in the future is being forecasted), the behavior of demand, and the possible existence of patterns (trends, seasonality, and so on), and the causes of demand behavior.

Demand Behavior

Demand sometimes behaves in a random, irregular way. At other times it exhibits predictable behavior, with trends or repetitive patterns, which the forecast may reflect. The three types of demand behavior are trends, cycles, and seasonal patterns.

A seasonal pattern is an oscillating movement in demand that occurs periodically (in the short run) and is repetitive. Seasonality is often weather related. For example, every winter the demand for snowblowers and skis increases, and retail sales in general increase during the holiday season. However, a seasonal pattern can occur on a daily or weekly basis. For example, some restaurants are busier at lunch than at dinner, and shopping mall stores and theaters tend to have higher demand on weekends. Figure 10.1(c) illustrates a seasonal pattern in which the same demand behavior is repeated each year at the same time.

Demand behavior frequently displays several of these characteristics simultaneously.

Time series methods are statistical techniques that use historical demand data to predict future demand. Regression (or causal) forecasting methods attempt to develop a mathematical relationship (in the form of a regression model) between demand and factors that cause it to behave the way it does. Most of the remainder of this chapter will be about time series and regression forecasting methods. In this section we will focus our discussion on qualitative forecasting.

Qualitative methods use management judgment, expertise, and opinion to make forecasts.

The Delphi method is a procedure for acquiring informed judgments and opinions from knowledgeable individuals using a series of questionnaires to develop a consensus forecast about what will occur in the future. It was developed at the Rand Corporation shortly after World War II to forecast the impact of a hypothetical nuclear attack on the United States. Although the Delphi method has been used for a variety of applications, forecasting has been one of its primary uses. It has been especially useful for forecasting technological change and advances.

Technological forecasting has become increasingly crucial to compete in the modern international business environment. New enhanced computer technology, new production methods, and advanced machinery and equipment are constantly being made available to companies. These advances enable them to introduce more new products into the marketplace faster than ever before. The companies that succeed manage to get a "technological" jump on their competitors by accurately predicting what technology will be available in the future and how it can be exploited. What new products and services will be technologically feasible, when they can be introduced, and what their demand will be are questions about the future for which answers cannot be predicted from historical data. Instead, the informed opinion and judgment of experts are necessary to make these types of single, long-term forecasts.

Time Series Methods

Time series methods are statistical techniques that make use of historical data accumulated over a period of time. Time series methods assume that what has occurred in the past will continue to occur in the future. As the name time series suggests, these methods relate the forecast to only one factor--time. They include the moving average, exponential smoothing, and linear trend line; and they are among the most popular methods for short-range forecasting among service and manufacturing companies. These methods assume that identifiable historical patterns or trends for demand over time will repeat themselves.

The Instant Paper Clip Office Supply Company sells and delivers office supplies to companies, schools, and agencies within a 50-mile radius of its warehouse. The office supply business is competitive, and the ability to deliver orders promptly is a factor in getting new customers and keeping old ones. (Offices typically order not when they run low on supplies, but when they completely run out. As a result, they

The 5-month moving average is computed from the prior 5 months of demand data as follows:

The 3- and 5-month moving average forecasts for all the months of demand data are shown in the following table. Actually, only the forecast for November based on the most recent monthly demand would be used by the manager. However, the earlier forecasts for prior months allow us to compare the forecast with actual demand to

The 5-month moving average in the previous figure smooths out fluctuations to a greater extent than the 3-month moving average. However, the 3-month average more closely reflects the most recent data available to the office supply manager. In general, forecasts using the longer-period moving average are slower to react to recent changes in demand than would those made using shorter-period moving averages. The extra periods of data dampen the speed with which the forecast responds. Establishing the appropriate number of periods to use in a moving average forecast often requires some amount of trial-and-error experimentation.

The disadvantage of the moving average method is that it does not react to variations that occur for a reason, such as cycles and seasonal effects. Factors that cause changes are generally ignored. It is basically a "mechanical" method, which reflects historical data in a consistent way. However, the moving average method does have the advantage of being easy to use, quick, and relatively inexpensive. In general, this method can provide a good forecast for the short run, but it should not be pushed too far into the future.

These weights reflect the company's desire to have the most recent data influence the forecast most strongly.

SOLUTION:

Exponential Smoothing

Exponential smoothing is also an averaging method that weights the most recent data more strongly. As such, the forecast will react more to recent changes in demand. This is useful if

The smoothing constant, α, is between 0.0 and 1.0. It reflects the weight given to the most recent demand data. For example, if α = 0.20,

which means that our forecast for the next period is based on 20 percent of recent demand (Dt) and 80 percent of past demand (in the form of the forecast Ft, since Ft is derived from previous demands and forecasts). If we go to one extreme and let α = 0.0, then

PM Computer Services assembles customized personal computers from generic parts. Formed and operated by part-time State University students Paulette Tyler and Maureen Becker, the company has had steady growth since it started. The company assembles computers mostly at night, using part-time students. Paulette and
Maureen purchase generic computer parts in volume at a discount from a variety of sources whenever they see a good deal. Thus, they need a good forecast of demand for their computers so that they will know how many computer component parts to purchase and stock.

The remainder of the monthly forecasts are shown in the following table. The final forecast is for period 13, January, and is the forecast of interest to PM Computer Services:

Exponential Smoothing Forecasts, α = .30 and α = .50

(Later in this chapter we discuss several quantitative methods for determining forecast accuracy.) When demand is relatively stable without any trend, a small value for α is more appropriate to simply smooth out the forecast. When actual demand displays an increasing (or decreasing) trend, as is the case in the figure, a larger value of α is better. It will react more quickly to more recent upward or downward movements in the actual data. In some
approaches to exponential smoothing, the accuracy of the forecast is monitored in terms of the difference between the actual values and the forecasted values. If these differences become larger, then α is changed (higher or lower) in an attempt to adapt the forecast to the actual data. However, the exponential smoothing forecast can also be adjusted for the effects of a trend.

In Example 10.3, the final forecast computed was for one month, January. A forecast for two or three months could have been computed by grouping the demand data into the required number of periods and then using these values in the exponential smoothing computations.

β is a value between 0.0 and 1.0. It reflects the weight given to the most recent trend data. β is usually determined subjectively based on the judgment of the forecaster. A high β reflects trend changes more than a low β. It is not uncommon for β to equal α in this method.

Notice that this formula for the trend factor reflects a weighted measure of the increase (or decrease) between the current forecast, Ft+1, and the previous forecast, Ft.

The formula for the adjusted exponential smoothing forecast requires an initial value for Tt to start the computational process. This initial trend factor is often an estimate determined subjectively or based on past data by the forecaster. In this case, since we have a long sequence of demand data (i.e., 12 months) we will start with the trend, Tt, equal to zero. By the time the forecast value of interest, F13, is computed, we should have a relatively good value for the trend factor.

The adjusted forecast for February, AF2, is the same as the exponentially smoothed forecast, since the trend computing factor will be zero (i.e., F1 and F2 are the same and T2 = 0). Thus, we compute the adjusted forecast for March, AF3, as follows, starting with the determination of the trend factor, T3:

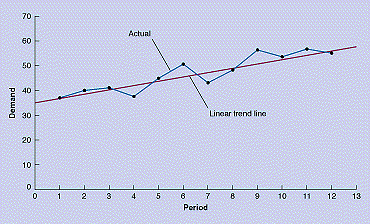
Linear regression is a causal method of forecasting in which a mathematical relationship is developed between demand and some other factor that causes demand behavior. However, when demand displays an obvious trend over time, a least squares regression line, or linear trend line, can be used to forecast demand.

A linear trend line relates a dependent variable, which for our purposes is demand, to one independent variable, time, in form of a linear equation:

exponential smoothing forecast methods will; that is, it is assumed that all future forecasts will follow a straight line. This limits the use of this method to a shorter time frame in which you can be relatively certain that the trend will not change.