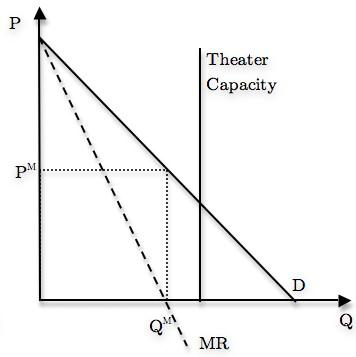
The guns canbe produced constant marginal cost
Department of Economics
Columbia University
2. A monopolist faces the (inverse) demand for its product: p = 50- 2Q. The monopolist has a marginal cost of 10/unit and a fixed cost given by F.
3. For profit-maximizing monopolies, explain why the boundaries on the Lerner Index are 0 and 1.
Answer: The Lerner Index equals (p - MC)/p. Because marginal cost is greater than or equal to zero and the optimal price is greater than or equal to the marginal cost, then 0 ≤ p - MC ≤ p. So the Lerner Index ranges from 0 to 1 for a profit-maximizing firm. As price gets higher, the Lerner Index approaches 1. As price gets lower, the index approaches zero.
6. An electric utility is going to use a block-pricing schedule. They plan to charge P1 for the first Q1 units and P2 for the subsequent units. The units sold at P2 are the total units sold, Q2, minus the total units sold at P1. The inverse demand curve is P = $100 - Q, and the marginal and average cost is $40. Use calculus to solve for P1, P2, Q1, Q2.
Answer: The profit equation for this utility is π = P1 (Q1) x Q1 + P2(Q2) x (Q2 - Q1) - 40 Q2. The derivative of profit with respect to Q1 is 100 - 2 x Q1 - 100 + Q2. The derivative of profit with respect to Q2 is 100 - 2 x Q2 + Q1 - 40. By setting these two derivatives equal to zero and substituting, Q1 equals 20 and Q2 equals 40. Substituting the quantities into the inverse demand curve, P1 equals $80 and P2 equals $60.
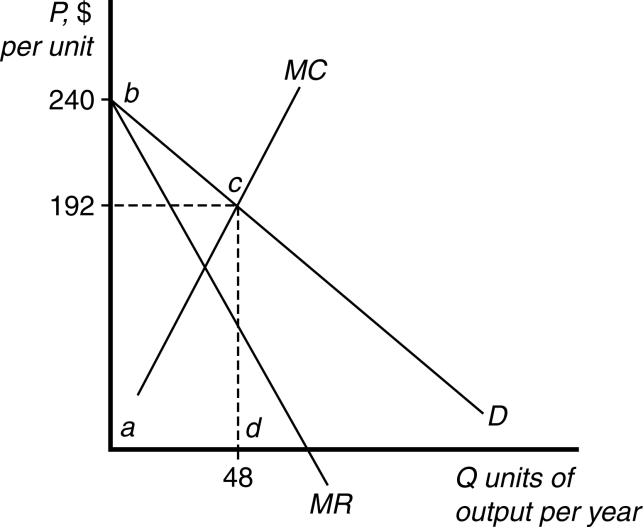
Answer: With perfect price discrimination, the monopolist sets MC p to determine the best output level. Costs are $4808. Revenue is the entire area under the demand curve from Q 0 to 48, or $10,368 (area abcd in Figure 12.1). Profits are $5560, and consumer surplus is zero.
| 4 Q | | 240 | |
|
| |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q | * | | ||||||||||||||||||
| R | | 192 | | 48 | | 1 | (240 | | 192) | |||||||||||
| 2 | ||||||||||||||||||||
| C | | |||||||||||||||||||
| | 200 | | 2 | | (48) | 2 | |
|
||||||||||||
| | | R | | C | | 10368 | | 4808 | | |||||||||||
QA = 100 - 2p
QB = 80 - 4p
Why is the weapons producer able to price discriminate? What price will
it charge to each country?
Answer: The firm can price discriminate because there are two identifiable segments with different elasticities. Since the two countries are at war, resale is doubtful. To solve, find marginal revenue for each and set equal to marginal cost of $10.
p = 50 - 0.5Q (Country A)
p = 20 - 0.25Q (Country B)
a. If the weapons producer can charge different prices to each country,
what price and quantity will it sell to each?
b. If the weapons producer cannot price discriminate, what price and quantity of guns will it sell to each country?
a. QA = 40, PA = 30
QB = 20, PB = 15
b. Write demand curves as
QA = 100 — 2p
QB = 80 — 4p
Total demand is
Q = 180 — 6p (for p<20)
Write inverse demand:
p = 30 — Q/6
MR = 30 — Q/3 = 10 = MC
Q = 60, p = 20(!)
But at p = 20, the firm is only selling to country A. The firm is better
selling at p=30 since only country A is buying!
On a graph:
d. Country A is indifferent, Country B is better because they can now
purchase weapons. e. Its easy to see in this case — the DWL to country A
is no different. The DWL to country B was 200 w/out price discrimination
(they didn’t purchase weapons), but with price
discrimination it is 50.
This is a case where price discrimination can actually reduce deadweight loss.
12. An electric utility is going to use a block-pricing schedule. They plan to charge P1 for the
first Q1 units and P2 for the subsequent units. The units sold at P2 are the total units sold,
recitation:
1. Ch. 11 question 24
6. Ch. 12 question 19
7. Ch. 12 question 22