The fourier transform ofsolution the fourier transform eisx dxb eisx dxb eisx eisbeisa example

UUNNIITT IIII

	F(s) =	2π 1 ∞ ∫ f (x) eisx dx

www.BrainKart.com

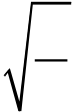
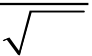
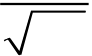
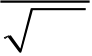
f (x) =

5.Fourier Cosine Transform:

f (x) =	0

EXAMPLES:

	f (x)		x ≤a		f (x)		−a ≤x ≤a	& a <x <∞
	f (x)		x >a		f (x)		−∞<x <−a	& a <x <∞

www.BrainKart.com

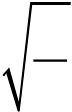
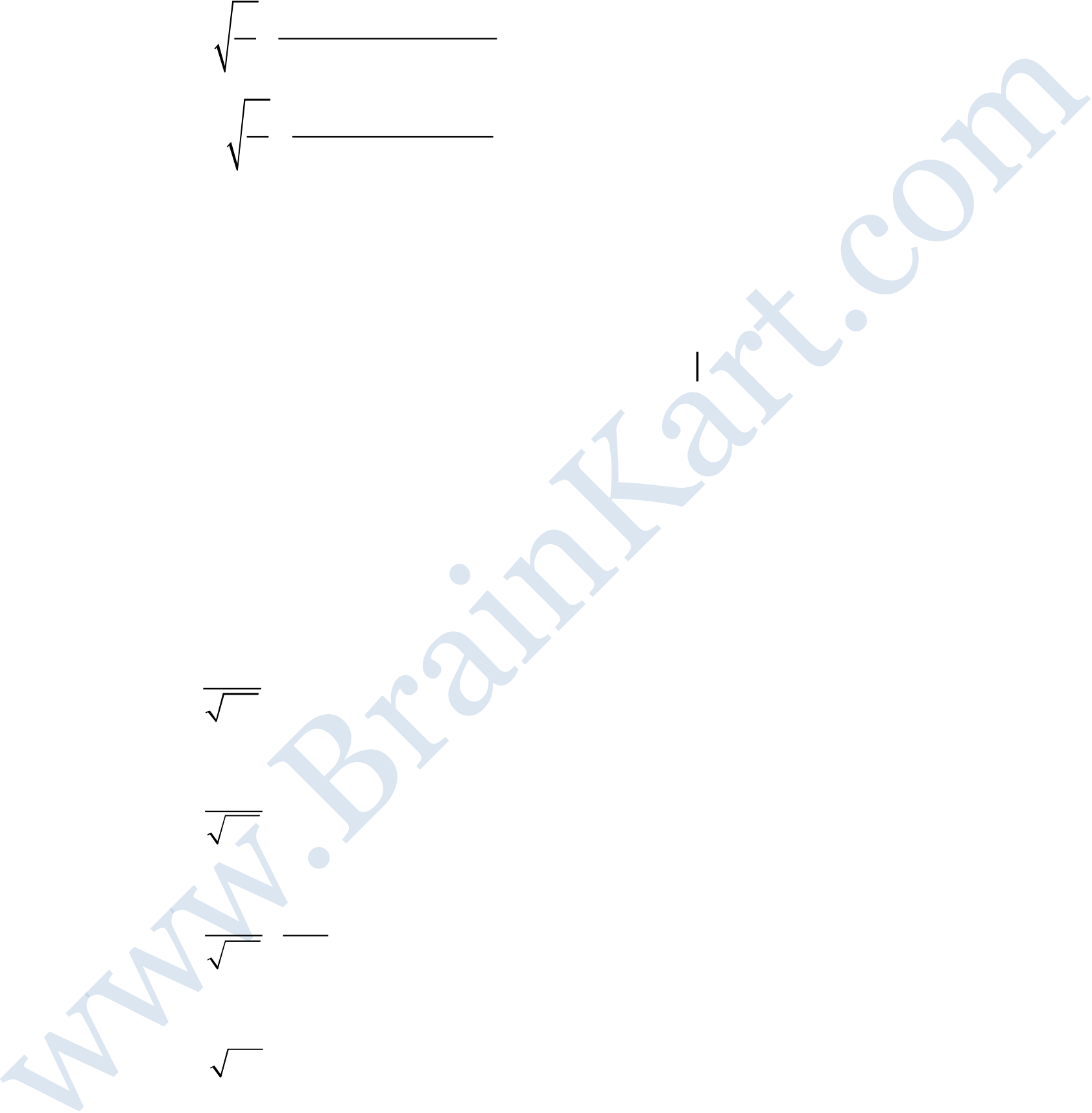
	f (x) defined by
		0, x <a f (x) = 1, a <x <b . 0,x>b
		0, x <a f (x) = 1, a <x <b . 0,x>b

www.BrainKart.com

∫ f (x) eisx dx

−∞

1 ei(k +s)x b
=2πi(k +s)    a
=1 2πi(k +s) 1 (ei(k +s)b−ei(k +s)a ).

EXAMPLE:

=	a 2		cos sx dx
=	a 2		cos sx dx
=	2 π	 sin sx  −cos sx a
=		2  
=

Find the Fourier transform of the function f (x) defined by

	F(s) =	−∞
	1 =1 ∫ (1−x2

)(cos sx +i sinsx )dx

www.BrainKart.com

MA2211 – TRANSFORMS AND PDE

	∞sin s −s coss  ∫ 0   s 3 cos sx ds = 				π
						f (x)
					4	f (x)		if	x ≤a
Put		we get,
∞sin s −s coss  s 				π1  4 f 2 
∞sin s −s coss  s 				π1  4 f 2 
π 1 2  =4 1 −2   


	∞sin s −s coss  s  3π ∫




Find the Fourier transform of				f (x) if			f (x)	if	x >a
∞sin t 2 π
∞sin t 2 π
			−∞
F(s) =			−∞

2.8 UNIT II

2 2 ∫(a −x )

By Fourier inverse transform,

2(

f (x) =

∞
12π ∫ −∞

2 

FOURIER TRANSFORM 2.9

Putx =0 we get,

=π(a)
4

2 ∞sint 2  
a 
∞sin t 2		π 4 (a)
∞sin t 2		π 4 (a)
	∫t 0
	(SELF RECIPROCAL)

If a transformation of a function called self reciprocal.

MA2211 – TRANSFORMS AND PDE

	∞ −1 (x −is )2 =1			−s
	∞ −1 (x −is )2 =1
	− s2 e 2 ∞		−1 (x −is )2
			−1 (x −is )2
	=

	Fc (s) =		∞ ∫f (x) cos sx dx 0
	=	a 2
	=	0a 1   2 π ∫cos (s +1)x +cos (s −1)x dx
	=	0a 1   2 π ∫cos (s +1)x +cos (s −1)x dx

Fc (s) =	2 π
=	2	∞ −ax
	2

=	2	e−ax						∞
	2	a2+s2(−acossx+ssinsx)
		a2+s2(−acossx+ssinsx)
						cosbx dx =	eax 


=	2	(0) −	1		(−a(1) +0)  
		(0) −	a2 +s2
			a2 +s2
	2	a		.
	π a2 +s2			.

EXAMPLE:

SOLUTION:

=	∞ 2 π ∫f (x) cos sx dx 0
=
=	2
=	π	s	 0
=
=	π  s  
=	π  s  

	−x 2	+isx
	2	+isx
∞ =1 Real part of ∫e 2π −∞	−1(x2−2isx) 2
	−1(x2−2isx+(is)2−(is)2) 2

2.14 UNIT II

Find the Fourier cosine transform of e−x	∞cos xt and deduce that ∫1 +t 0 2	dt = πe−x . 2

FOURIER TRANSFORM 2.15

2		
2
π
	 ax ∵ ∫e	cosbx dx =
	 ax ∵ ∫e	cosbx dx =

By inverse Fourier cosine transform,

∞

2 2 1

π 0∫1 +s2 cossx ds

∞

EXAMPLE:

	f (x)
	f (x)

SOLUTION:

www.BrainKart.com

=
1 sin(s −1)x =2π s −1	−
1 sin(s −1)x =2π s −1	−	s +1	 
=
=1 2π sin(s −1)a −sin(s +1)a .
	
	

Find the Fourier sine transform of

	=	2−coss +sin s −sin 2s +coss +sin s 
	=

MA2211 – TRANSFORMS AND PDE

www.BrainKart.com

d	2	∫∂e 0 s x	
ds Fs (s) =	2
ds Fs (s) =	π

	Fs (s) = =		2 1	(2)
	Put s =0	in (1) we get,
	Fs (0) =0


	Put s =0

EXAMPLE:

		the	Fourier	sine	transform	of	e−ax , a >0 .	Hence	deduce
		s	π −ax

SOLUTION:

Inverse Fourier sine transform,

f (x) =	2		∞
	2
	π
=		2		2	s
=				π	s2 +a2
=	2 ∞ π0 ∫		s			sin sx ds
=	2 ∞ π0 ∫		s2 +a2			sin sx ds

sin sx ds =	2

MA2211 – TRANSFORMS AND PDE
www.BrainKart.com

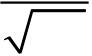
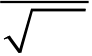
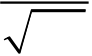
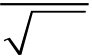
If F(s) is the Fourier transform of f (x), then

∞ ∞

EXAMPLE:

F(s) =	−∞	f (x) eisx dx

=	2π∫ − a
2π −a ∫sin sx dx
=	1 a

2.20 UNIT II

By inverse Fourier transform,

f (x ) =
=	∞2π∫	2 sinsa  −isx
	∞2π∫
	−∞
 s (cossx −i sin sx )ds  −∞


			i ∞sin sa  π∫   s −∞


1∞sin sa  =π2 ∫0  s cossx ds −0




0  s cossx ds = 