The anti-hebbian learning rule used update the weights okxk
Department of Computer Science
COMP528 Individual coursework
Assignments 3 and 4
Parallel geometric attack on neural key exchange protocolAlexei Lisitsa
alexei@liverpool.ac.uk
| Assignment 1 | |
|---|---|
| Assignment 2 | |
| Assignment 3 |
|
| Assignment 4 |
|
| TOTAL | |
1 Introduction
This exercise is on programming of analysis of secret key exchange protocol based on artificial neural networks. No preliminary knowledge of key exchange protocols or neural networks is required. All necessary concepts are explained in this section.
2.1 KKK protocol
In this section we briefly describe a variant of KKK scheme which uses an anti-Hebbian learning rule and for which a genetic attack has been first considered in [2].
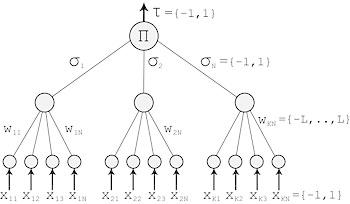
Figure 1: Parity machine
Here we describe briefly the geometric attack. The attacker constructs a neural network C with the same structure as these of A and B and randomly initializes its weights. At each step she trains C with the same input as the two parties, and updates its weights with the following rules:
• If A and B have different outputs OA̸= OB, then the attacker doesn’t update C• If all A, B and C have the same outputs OA= OB= OCthen the attacker update C by the usual learning rule.
How to make attacks less successfull?
In [3] it has been argued that increasing the range of weights in the neural networks, that is a parameter L, would provide a defense against geometric attacks and in [4] the argument has been extended to other types of attacks including genetic one. The efficiency of such a defense is based on the fact that synchronization time grows proportionally to L2, while success rate of the attacks drops exponentially.
• execution on single host, or a cluster (with reasonable resources requested);
• online or offline attack.
Marking scheme
The submitted solutions will be evaluated separately for Assignments 3 and 4 by the following criteria splitted in two parts:
Main Part
Submission
The work must be submitted electronically by going to the Web page at
https://cgi.csc.liv.ac.uk/login.php
Section 8
and
[1] I. Kanter, W. Kinzel, E. Kanter, Secure exchange of information by synchronization of neural
networks, Europhys. Lett., 141, 2002.
[4] A. Ruttor, W. Kinzel, R. Naeh, I. Kanter, Genetic Attack on Neural Cryptography, arXiv:cond- mat/0512022 v2, June 2006.
[5] http//rfic.ucsd.edu/chaos





