Testgraph defined its incidence matrix graphs are defined

Graph theory, test

Graph G1 is defined of its incidence matrix:

0 0 0 0 0 0 1 0 1 1 1 0 0 0;

0 0 0 1 0 0 0 0 0 1 0 1 1 0;

a) G_2 is an Eulerien graph;

b) G_1 is an Eulerien graph.

Vertex 8 has odd degree so it is not Eulerien graph

G_2

c) G_4 has an Eulerien path;

d) G_3 has an Eulerien path.

G_4

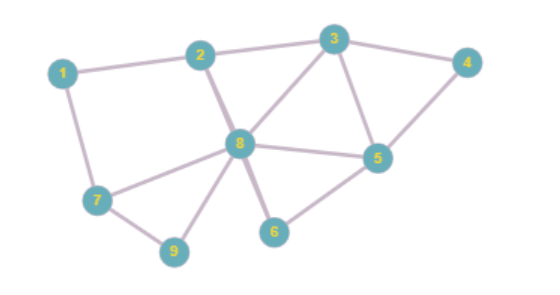vertex 7 have odd degree

Matrix:

0 0 1 0 1 1;

1 1 0 0 0 0.

1) none of them; 2) G^{}_0; 3) G_1; 4) all three; 5) G_1 amd G_2; 6) G^{}_0 and G_1; 7) G_2; 8) G^{}_0 and G_1.

graph G_1

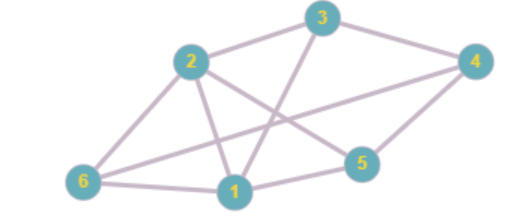
Answer: 2

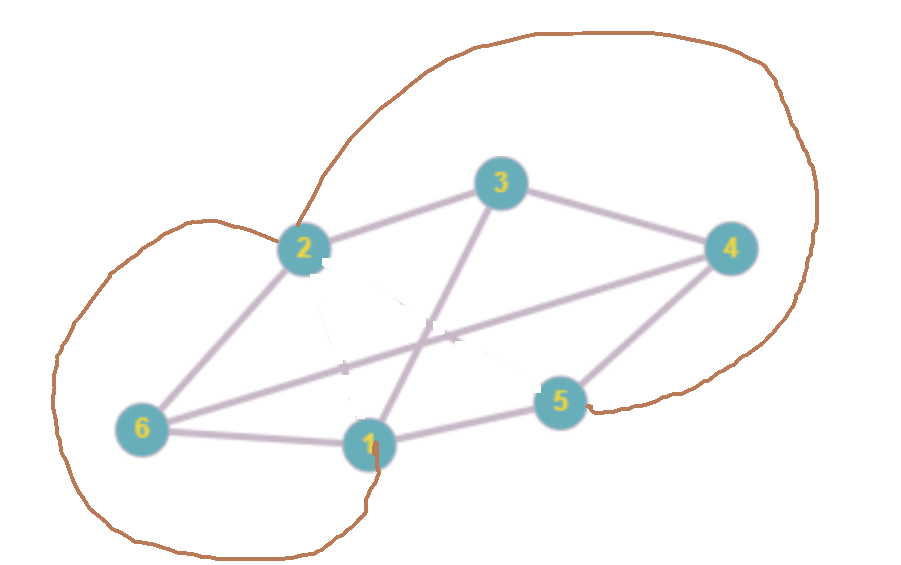
Graph is given:

a) {1,5} ∈ E_+; b) {1, 4} ∈ E_+.

1) both facts; 2) (b); 3) none of them; 4) (a).

Step by step solution: ..........

Answer: .....

1) �(G)=6; 2) �(G)=3; 3) �(G)=0; 4) �(G)=1; 5) �(G)=5; 6) �(G)=7; 7) �(G)=2; 8) �(G)=4.

Step by step solution: ..........

1 0 0 1 1 0 0 0;

0 0 0 1 0 1 1 0;

1) C_1 and C_3;

2) C_1;

7) C_2;

8) C_2 and C_3.

C_2=(1,4,5,2,5,3,4,1): vertices 5th visited more than once.

C_3=(1,2,5,3,4,5,1): vertices 5th visited more than once.

c) graph G has an Eulerien cycle.

1) (b); 2) none of them; 3) (a) and (c); 4) (a) and (b); 5) all facts; 6) (a);; 7) (b) and (c); 8) (c).

Planner Graph : A graph is said to be planar if it can be drawn in a plane so that no edge cross

So it is planner Graph as no edges are crossed each other.

A tree could be saved into the following array:

1) (2,7,2,3,5,7); 2) (2,7,2,5,6,8); 3) (2,1,1,8,3,2); 4) (2,1,1,8,2,2); 5) (2,1,1,8,8,2); 6) (2,6,2,5,5,7); 7) (2,7,2,5,8,7); 8) (2,1,1,8,2,3).

1 is parent of 2 no of vertices

Answer: 4

3) {{1,4},{1,5},{1,8},{2,4},{2,6},{2,7},{2,8}};

4) {{1,2},{2,4},{2,5},{3,7},{5,7},{5,8},{6,7}};

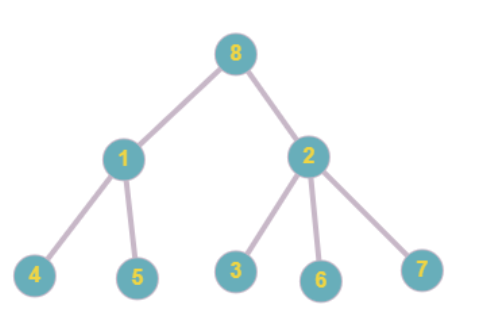
Answer: 5