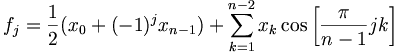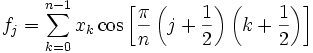Symmetric convolution and the discrete sine and cosine transforms ieee trans

Discrete cosine transform - Wikipedia, the free encyclopedia 第 1 頁，共 4 頁

Discrete cosine transform

Contents
1 Applications
2 Formal definition
2.1 DCT-I
2.2 DCT-II
2.3 DCT-III
2.4 DCT-IV
2.5 DCT V-VIII
3 Inverse transforms
4 Computation
5 References
6 External link

Applications

Formal definition

Formally, the discrete cosine transform is a linear, invertible function F : Rn-> Rn (where R denotes the set

Some authors further multiply the x0 and xn-1 terms by √2, and correspondingly multiply the f0 and fn-1 terms by 1/√2. This makes the DCT-I matrix orthogonal (up to a scale factor), but breaks the direct correspondence

The DCT-II is probably the most commonly used form, and is often simply referred to as "the DCT".

Because it is the inverse of DCT-II (up to a scale factor, see below), this form is sometimes simply referred to as "the inverse DCT" ("IDCT").

Some authors further multiply the x0 term by √2 (see above for the corresponding change in DCT-II). This makes the DCT-III matrix orthogonal (up to a scale factor), but breaks the direct correspondence with a real-even DFT of half-shifted output.

The DCT-IV matrix is orthogonal (up to a scale factor).

(The trivial real-even array, a length-one DFT (odd length) of a single number a, corresponds to a DCT-V of length n=1.)

Inverse transforms

Computation

Although the direct application of these formulas would require O(n2) operations, as in the fast Fourier transform (FFT) it is possible to compute the same thing with only O(n log n) complexity by factorizing the computation. (One can also compute DCTs via FFTs combined with O(n) pre- and post-processing steps.)

� Matteo Frigo and Steven G. Johnson: FFTW, http://www.fftw.org/. A free (GPL) C library that can compute fast DCTs (types I-IV) in one or more dimensions, of arbitrary size. Also M. Frigo and S. G.

Johnson, "The Design and Implementation of FFTW3 (http://fftw.org/fftw-paper-ieee.pdf)," Proceedings of the IEEE93 (2), 216–231 (2005).

Retrieved from "http://en.wikipedia.org/wiki/Discrete_cosine_transform"

Categories: Digital signal processing | Fourier analysis