Subspace intersection & span answers and explanation
Subspace Intersection & Span Step by step Solution with Explanation
Your question:
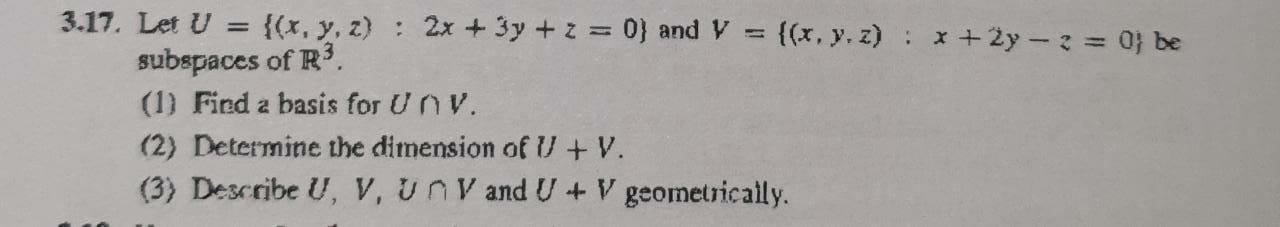
Let U = {(x, y, z) : 2x + 3y +z = 0} and V = {(x, y, z) : x +2y - 2 = 0} be subspaces of R3 (1) Find a basis for U V. (2) Determine the dimension of U + V. (3) Describe U, V, un V and UV geometrically.
Subspace Intersection & Span Answers and Explanation
1. Basis for U ∩ V (Intersection of U and V):
We need to find vectors that belong to both U and V.
3x + 5y = 0
x = -\frac{5}{3}y
satisfies both equations (where y is any scalar).
Basis for U ∩ V:
However, to know for sure, we'd need the exact dimensions of U and V (which depends on how many directions each plane allows for movement).
The formula captures this relationship:
dim(U ∩ V): We found a single basis vector for the intersection, so dim(U ∩ V) = 1.
Applying the formula:
U ∩ V: The line of intersection where these two planes meet. It's spanned by the vector (-5, 3, 1).
U + V: Based on the dimensions and the fact that the intersection is not just the zero vector, U + V likely spans the entire space ℝ³. However, without knowing the exact dimensions of U and V, we can't say for certain.
U: Plane defined by 2x + 3y + z = 0
V: Plane defined by x + 2y - z = 0





