Your Question:

Parametric Curve Derivative of Log functions please explain your steps and show what laws and rules you use so i can understand and learn thank you very much i will give you thumbs up!

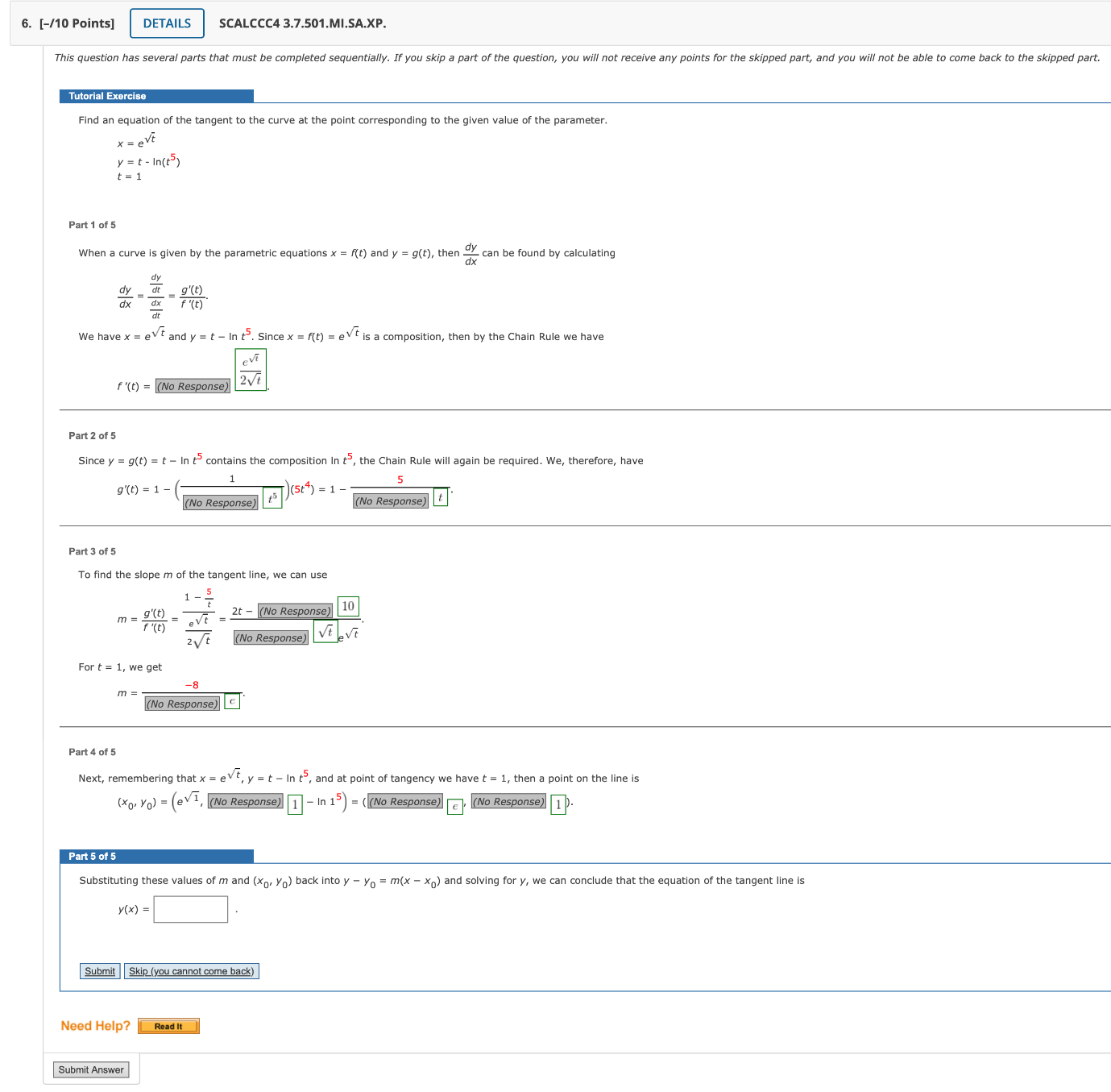Step By Step Answers with Explanation

Sure. Here is a step-by-step explanation of how to calculate the parametric curve derivative of a log function with 450 words:

y = t - \ln(t^5)

In this example, the parameter is t. The first equation defines the x-coordinate of any point on the curve in terms of t, and the second equation defines the y-coordinate of any point on the curve in terms of t.

This rule tells us that the derivative of the exponential function is itself. Applying this rule to the first equation, we get:

\frac{dx}{dt}=\frac{d}{dt}\left[e^{\sqrt{t}}\right]=e^{\sqrt{t}}\cdot\frac{1}{2\sqrt{t}}=\frac{e^{\sqrt{t}}}{2\sqrt{t}}

Step 3: Use the chain rule to differentiate any composite functions in the parametric equations.

The chain rule is a rule of differentiation that allows us to differentiate composite functions. A composite function is a function of a function. For example, the function ln(t5) in the example above is a composite function. The inner function is t5, and the outer function is the logarithmic function.

Step 4: Divide the derivative of the y-equation by the derivative of the x-equation to find the slope of the tangent line to the parametric curve at any point.

The slope of the tangent line to a parametric curve at any point is equal to the derivative of the y-equation divided by the derivative of the x-equation.

Therefore, the slope of the tangent line to the parametric curve at any point is:

m = \frac{dy}{dt}/\frac{dx}{dt} = \frac{1 - \frac{5}{t}}{\frac{e^{\sqrt{t}}}{2\sqrt{t}}} = \frac{2t - 5}{\sqrt{t} \cdot e^{\sqrt{t}}}