Soft condensed matter eugene terentjev elements fluid dynamics

Soft Condensed Matter
Eugene Terentjev

• Elements of fluid dynamics, focusing on low-Re regime;• Viscoelasticity, focusing on relaxation/damping;
• Brownian motion, focusing on diffusion & activation;• Interactions, focusing on fluid-mediated and interfaces;• Self-assembly, focusing on equilibrium structures;• Elements of polymer physics: single chain in solution, phase equilibrium, networks and rubber elasticity

Pierre-Gilles de Gennes
Nobel Prize in Physics 1991

In his Nobel Prize lecture he identifies the following key topics as the central players in soft condensed matter:
•	Polymers
•
•
•
		3

What do we mean by
Soft Condensed Matter?

Most of the biological systems, from peptides and proteins to cells, to organisms fall into the “soft matter” category

The predominant techniques we use are classical mechanics and statistical physics

‘a discipline still waiting to be adequately defined’

(Cotterill – Biophysics an Introduction).

TMV	Cell Membrane

of biological phenomena that require soft matter physics.

	6

o no vorticity (electromagnetic analogy)

7	7

ρ i
Re-arrange:	∇	2	v	= ∇			div	v	−		curlcurl						v
					2	v i			i	p		+	f		ext
Full (convective) time derivative gives the total acceleration: Dv i ( x , ) =														d x		∂x
														d t		∂x

Fluid rotates about cylinder axis			2
v = = η σ 2 xd 1 + 1		z
					A
	
			still:	(v	⋅∇	)v	=
So generally, we have for the axial shear stress			still:	(v	⋅∇	)v	=
= r d dT r dr r ω() Solution: =C 1 + C 11 r 2 2

																													2
L.H.S.														(vθ	⋅∇	)	vθ		=	0				z					A	1
Steady-state, so ∂v/∂t = 0
Velocity ┴ gradient, so											still:
But the radial component of convective acceleration is present:																			[(v		⋅∇		)	v	]r
R.H.S.																			[(v		⋅∇		)	v	]r
There are no forces along θ																				d P			=		ρ θv 2 r
But there has to be a radial gradient:																				d P
But there has to be a radial gradient:																				d r
Also, the laminar friction term in 2D polar coordinates takes the form:
	d	2		vθ	+	1	d	vθ		−		vθ
	d		r			r	d		r	−		r	2														c 2
which has the solution:																		=ω⋅				r		=		cr 1+	c 2
which has the solution:																		=ω⋅				r		=		cr 1+	r	12

σ		1)
θr	vθ(r)	2) Vortex flow (has zero vorticity)
But no contribution to the Navier-Stokes eq.		2) Vortex flow (has zero vorticity)
But no contribution to the Navier-Stokes eq.		13

Laminar friction term is
Pressure gradient imposed: ∇			xP		= ∆P L / )
There are no other forces along x
All we are solving here is:	dv 2		x	=
All we are solving here is:	dy	2		=

On solid surface: no-slip boundary

condition is assumed

	)			Find the two constants, or just write:


				F					∆Pd b
The total rate of flow:	Q	=	∫	x			2
The total rate of flow:	Q	=	∫	v d x Area	⊥	x		14

Example: blood flow

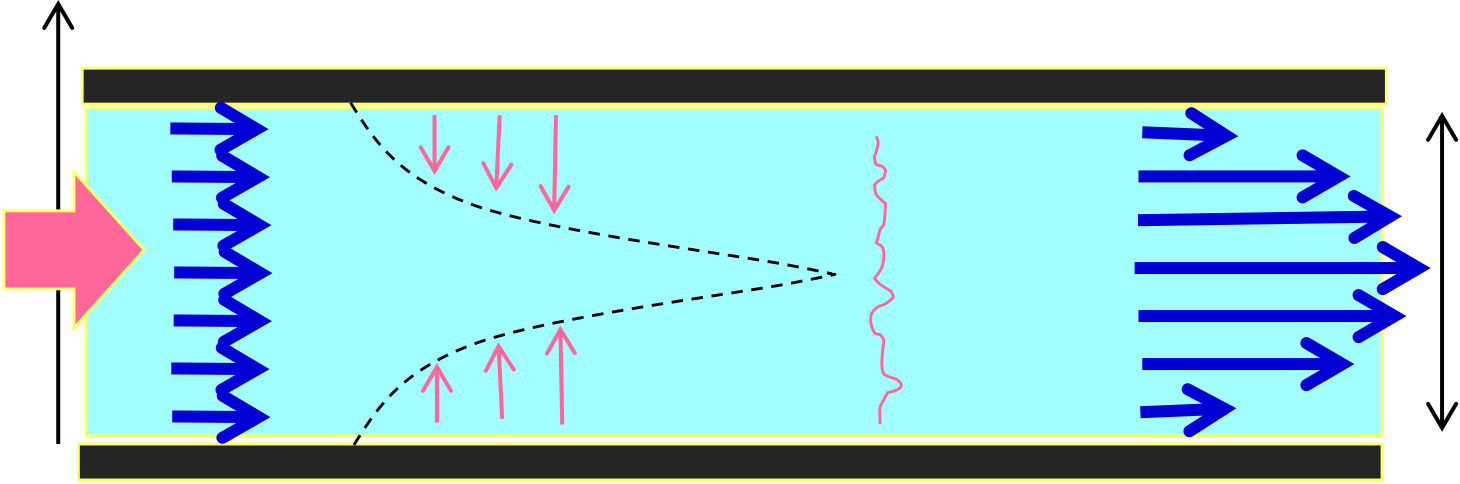
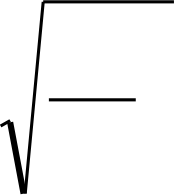
Onset of flow: diffusion of vorticity

Definitely t-dependence: ∂v/∂t ≠ 0							Boundaries move δ u 0 ie t
But velocity ┴ gradient, so
We only have:	R.H.S.
We only have:	R.H.S.						x
Since there is neither a pressure gradient , nor any external force along x, the motion is driven by the boundary condition!							x
							as: iρωv=η ∂ 2 v
So we are solving:		ρ	η	∂	2	v	as: iρωv=η ∂ 2 v
So we are solving:				∂y		2	∂y 2

which gives the “wave vector”

The fluid flow is a decaying wave on both sides of the plate:	v	=	u 0	⋅	e	−	y	/δ	⋅	e	i	[ωt y	/ ]	18

Reynolds’ Number

A heuristic argument gives a feel for this number for a simple geometry of a spherical particle.
Re =
	η

More generally (i.e. not for a sphere) R will be some characteristic length scale of the object or flow geometry.

The viscous stress is

R
v