Sha based the hash function and its design closely models

Chapter 6

New HASH Function

6.1.1 Authentication Requirements

In the context of communication across a network, the following attacks can be identified:

111

including insertion, deletion, transposition, and modification.

• Destination repudiation: Denial of receipt of message by des- tination.

6.1.2 Authentication Functions

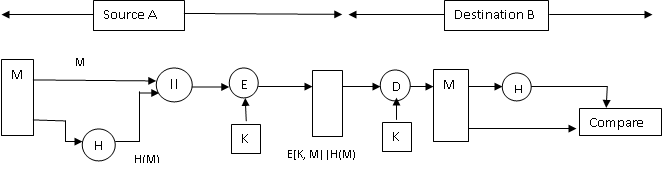
plaintext of the message. In addition, we may say that′B′is assured that the message was generated by′A′. The message must have come from′A′because′A′is the only other party that possesses secret key′K′and therefore the only other party with the information necessary to construct ciphertext that can be decrypted with′K′. Furthermore, if message′M′is recovered, B knows that none of the bits of′M′have been altered, because an opponent that does not know′K′would not know how to alter the bits in the ciphertext to produce desired changes in the plaintext

• Message Authentication Code (MAC): A function of the mes-sage and a secret key that produces a fixed-length value that serves as authentication. An alternative technique involves the use of a secret key to generate a small fixed-size block of data, known as a cryptographic checksum or MAC that is appended to the message. This technique assumes that two communication parties say′A′and′B′, share a common se-cret key′K′. When′A′has a message to be sent to′B′, it calculates the MAC as a function of the message and the key. The message and the MAC are transmitted to the intended recipient′B′. The recipient performs the same calculation on the received message, using the same secret key to generate a new MAC. The received MAC is compared to the calculated

Figure 6.1: Encrypt message plus hash code

Figure 6.2: Encrypt hash code with shared secret key

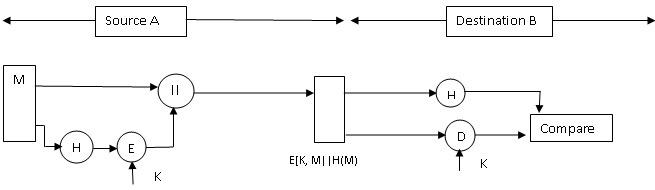
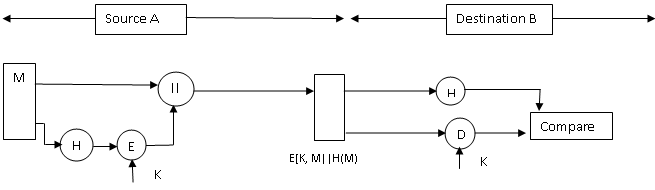
This reduces the processing burden for those applications that do not require confidentiality. Fig.6.3 shows hash function generator using sender’s private key in public key cryptography

Figure 6.4: Encrypt result of encrypted hash code with shared secret key

116

the fixed length hash value. The hash value is appended to the

message at the source at a time when the message is assumed or

have the following properties.

• H can be applied to a block of data of any size.

117

x such that H(x) = h. This is referred as the one-way prop-

• It is computationally unfeasible to find any pair(x, y) such

that H(x) = H(y). resistance.

• Weak collision resistance: For any given block x, it is compu-tationally unfeasible to find y ̸= x with H(y) = H(x). The level of effort required is 2n.

• Strong collision resistance: It is computationally unfeasible to find any pair (x, y) such that H(x) = H(y). The level of effort required is 2n/2.

119

6.2.4 Secure Hash Algorithm (SHA)

121

• Block ciphers do not possess the properties of randomizing functions. For example they are invertible. This lack of ran-domness may lead to weaknesses that can be exploited

• The overall structure of the hash function is one that has been shown to be resistant to the usual attacks on block cipher based hash codes.

122

• The given is a message and its n-bit hash result, the expected workload of finding a second message that hashes to the same value is of the order of 2nexecutions of Whirlpool.

• It is unfeasible to detect systematic correlations between any linear combinations of input bits and any linear combinations of bits of the hash results or to predict what bits of the hash re-sult will change the value when certain input bits are flipped. This means resistance against linear and differential attacks.

6.3.1 Hash Function Structure

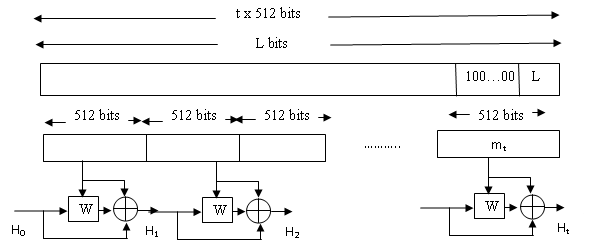
Given a message consisting of a sequence of blocks m1, m2, · · · mt, the Whirlpool hash function is expressed as follows:
H0 = Initial Value
Hi = W(Hi−1, mi) + Hi−1 + mi
Ht = Final Hash Code value.

the overall processing of a message to produce a digest.

• Append length: A block of 256 bits is appended to the mes- sage. This block is treated as an unsigned 256-bit integer (most significant byte first) and contains the length in bits of the original message (before the padding). The outcome of the first two steps yields a message that is an integer multi- ple of 512 bits in length. In Fig.6.8, the expanded message

125

Whirlpool uses a block cipher that is specifically designed for use in the hash function. The block cipher W, which has a similar structure and uses the same elementary functions as AES, uses a block size and a key size of 512-bits. Although W is similar to AES, it is not simply an extension. AES operates on a state of 4×4 bytes, whereas W operates on a state of 8×8 bytes. W uses a row-oriented matrix whereas AES uses a column-oriented matrix.

A comparison between AES and W is presented in Table 6.2

127

The substitute byte function (SB) is a simple table lookup that provides a nonlinear mapping. W defines a 16 × 16 matrix of byte values, called an S-box that contains a permutation of all possible 256, 8-bit values. Each individual byte of c-state is mapped into a new byte in the following way:

128