Respectively the intersection point the two tangent lines

Business Mathematics II –MATH221

Spring 2019

2. Find the intersection point of the two tangent lines, if any.

Solution:

The equation of tangent line is,

y = 1 – x, for x = 0,

Consider the following demand, supply and total cost functions:

Demand function: p = 100 e^{− 0.05 q}

Solution:

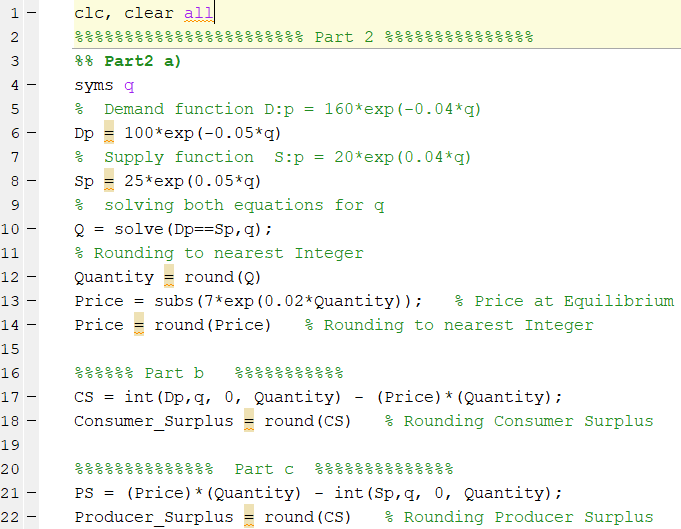
2. Calculate the consumer surplus.

We have to find the area under demand curve to get Consumer Surplus for this we need to integrate Demand curev w r t Quantity from q = 0 to Equilibrium

Quantity and then subtract it from area (Price)x(Quantity) at equilibrium

The Producer surplus is 881.

3. Using Matlab function “fmincon”, find the maximum and minimum of the function f(x,y).

Solution:

The critical point is -3 for the function.

2. Plot the function in the 3-D graph in MATLAB.

Part 4

Suppose that a restaurant has certain fixed costs per month of $5000. The fixed costs could be interpreted as rent, insurance etc. The marginal cost function of the restaurant is given by:

Solution:

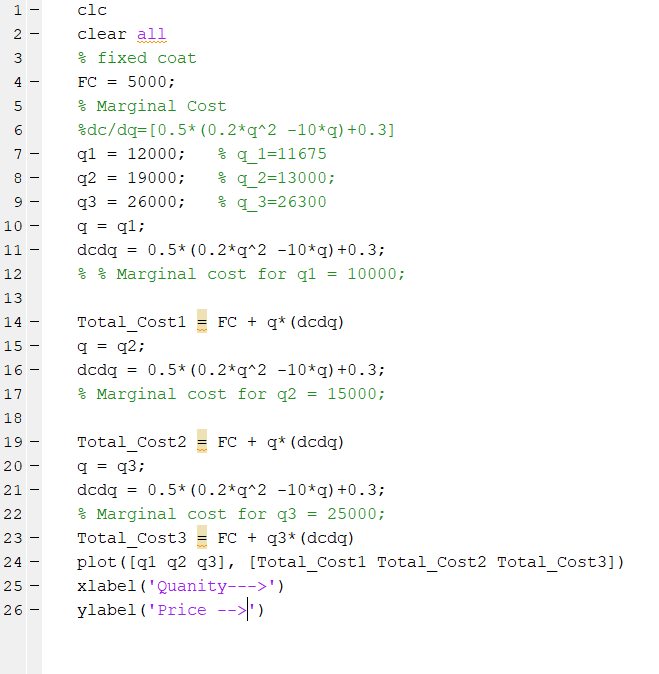
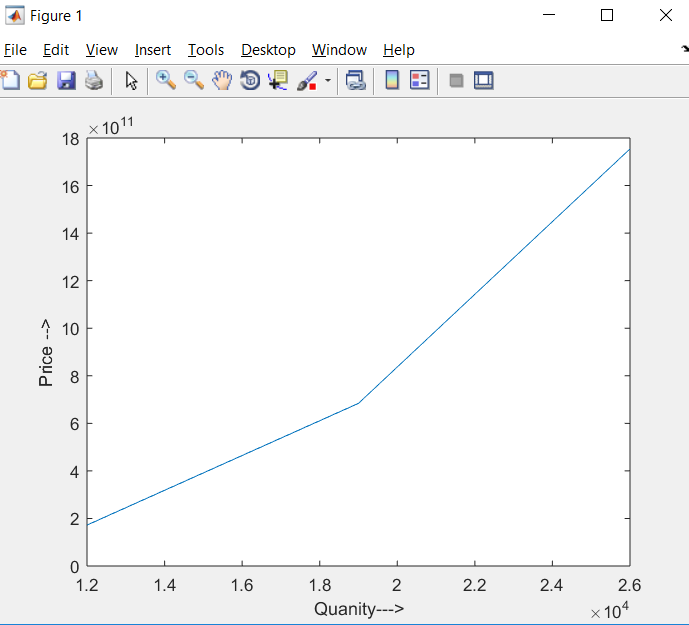
Total cost is increasing with the increase in the quantity. As it is observed from the graph of the function plotted between price and quantity.