Moreover cosb cosb cosb aas expected the definition cos

International Baccalaureate

MATHEMATICS
Analysis and Approaches (SL and HL)
Lecture Notes


	TRIANGLES – THE SINE RULE - THE COSINE RULE	...………………… 5
	APPLICATIONS IN 3D GEOMETRY – NAVIGATION ……..…………………….. 16 THE TRIGONOMETRIC CIRCLE – ARCS AND SECTORS …………………….. 22 SIN, COS, TAN ON THE UNIT CIRCLE – IDENTITIES ………………………… 29 TRIGONOMETRIC EQUATIONS ………………………………………………………….….. 38 TRIGONOMETRIC FUNCTIONS ………………………………………………………………. 48

TOPIC 3: GEOMETRY AND TRIGONOMETRY		Christos Nikolaidis
3.1	THREE DIMENSIONAL GEOMETRY	Christos Nikolaidis

d	AB		(x	1		x )	2		(y 1		y )	2		(z	1		z )

while the midpoint of the line segment AB is given by

M(	x	1 2	x	2	,		,	z		z	2

EXAMPLE 1

Let A(1,0,5) and B(2,3,1). Find

(a)	d	AB						2		(0		
(b)	d	OB		2	2		3	2		1	2	
(c)	d	OB		2	2		3	2		1	2	5 1 2	) i.e. M( 2 3 , 2 3 ,3 )
(c)	M( 1 2 2 , 0 3										,
(d)	M( 1 2 2 , 0 3										,

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

Cuboid

Vxyz

S	2xy		2yz		2zx

V			(height)

S (sum of areas

of the faces)

Vπr2h

S	2πrh	

Cone

S	πr L		πr 2

where

L		r	2		h

Sphere

V

S4πr2

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

EXAMPLE 2
The volume and the surface area for the following solids

Cube of side x
x

Cube:	V			S	6x	2
Cuboid of square base:	V	x2	y	S

Solution						πr2h				25		h 25 π r 2				50r
(a)	V		πr2h			πr2h				25		h 25 π r 2
(b)	S		2πrh		2πr 2			2πr 25 π r 2					2π	r	2

(a)

S

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

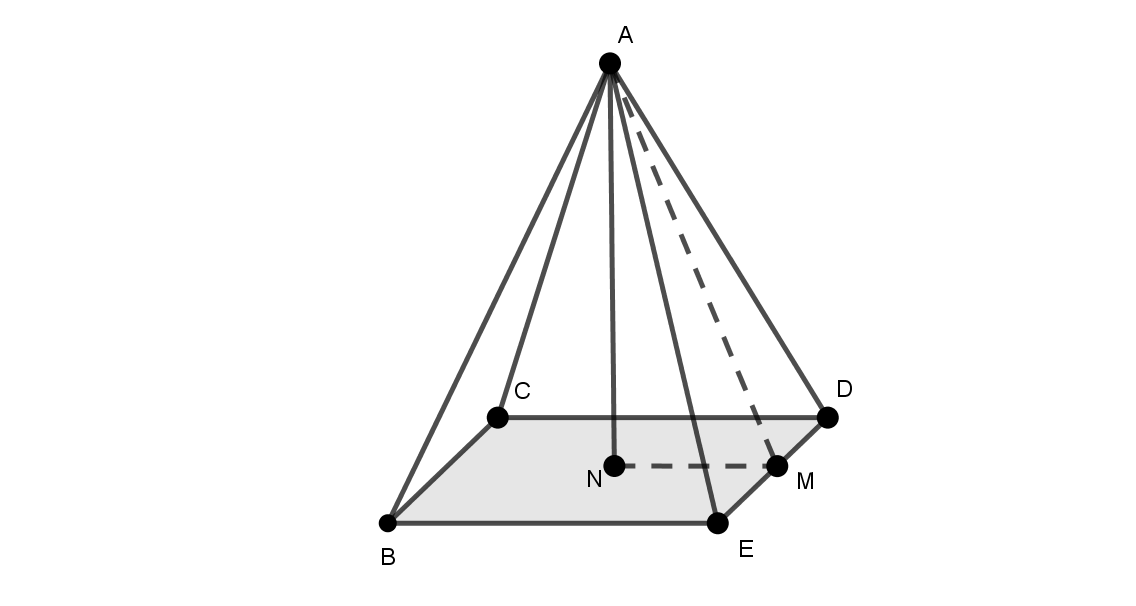
EXAMPLE 5
Find the volume and the surface area of a right pyramid of square base of side 6 and vertical height 4.

For the slant height AM we use the Pythagoras theorem on ANM.

AM	2		AN	2		NM	2		AM	2		4	2		3	2		AM 5

A			1 2			ED		AM		1 2		6			5	
The volume is	V												(height)					=	1 3		6	2		4	
The surface area is	S		(area of square base)+4A = 62+4×(15 ) =96

Notice about the angles between lines and planes:

Angle between line AM and plane BCDE = angle AMN

TOPIC 3: GEOMETRY AND TRIGONOMETRY		Christos Nikolaidis
3.2

B		b
B	θ c

sinθ = a b = hypotenuse

cosθ = a c = hypotenuse

It also holds

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

We can also confirm Pythagoras’ theorem:

=3 2



Every angle has a fixed sine, cosine and tangent. For example

sin30o = 1 2,

cos30o =

3
2,

For example, if sinθ = 1 2	then	θ = sin-1 1 2 = 30o

A + B = 90o

A + B = 180o

	Christos Nikolaidis

sinθ

1
2

2
2

Hence,

1 
3

1 2

If sinθ = 0.5		θ = sin-1 0.5 = 30o
If cosθ = 0.3	then

e.g.	sin30o = 0.5,
e.g.	cos30o =	3/2

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

B		a	b

B	2	104.5o	3
B		4	28.9o

	3 sin46.64.13	2 sin28.94.13

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

c	90o	C
B	a	C
b =
sinB		sinB

Also,	a	2		b	2		c	2		2bc cos90	o



-2c

2ca cosB

c

b a

	Christos Nikolaidis

Roughly speaking

If we know	we use
(three sides) OR (two sides and an included angle)
otherwise

B	2	4	3	C

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

Notice: We may sometimes have no solutions at all. For example, if a=10, b=3, c=2 it is not possible to construct such a triangle! Indeed, the cosine rule gives us cosA = -7.25 which is not possible!

B	2	104.5o	3

BC = 22 + 32 - 12 cos 104.5o = 16

B		104.5o	3	C

AB
sin 28.9

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

EXAMPLE 6 (given two sides and a non-included angle)

B		3
B		3

We use the sine rule

3 sin 46.6 =
Hence,

Notice: In fact, we obtain two values for C.

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

EXAMPLE 7 (given two sides and a non-included angle)

5		4
B

CASE (1): If C = 38.7o then

A΄ = 180o - 30o - 141.3o, thus A΄ = 8.7o

and then

	Christos Nikolaidis

We may, sometimes, obtain no solution at all.

EXAMPLE 8 (given 2 sides and a non-included angle)

B		a	1
B		a	1

We use the sine rule:

1 sin 30=

5	4	4

B		C

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

We can derive two similar versions for this formula:

Area = 1 ab sinC 2

Area = 1 ac sinB 2

EXAMPLE 9
Look at again the triangle in example 1:

B			3
B	46.60	4	28.9o

Area =	1 2 4 sin46.6o2
Area =	1 3 4 sin28.9o2

		Christos Nikolaidis
3.3

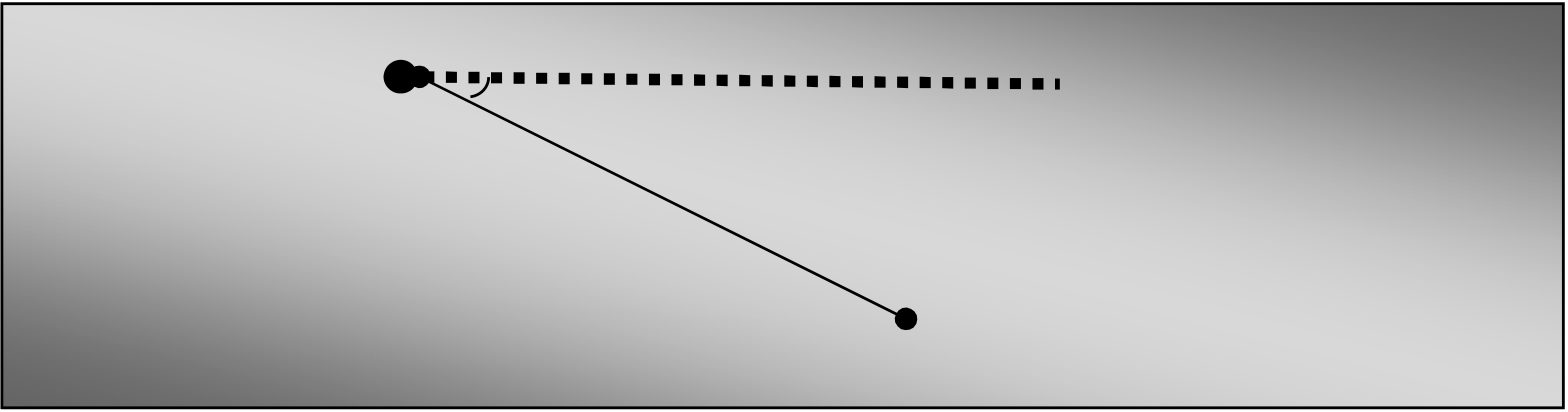
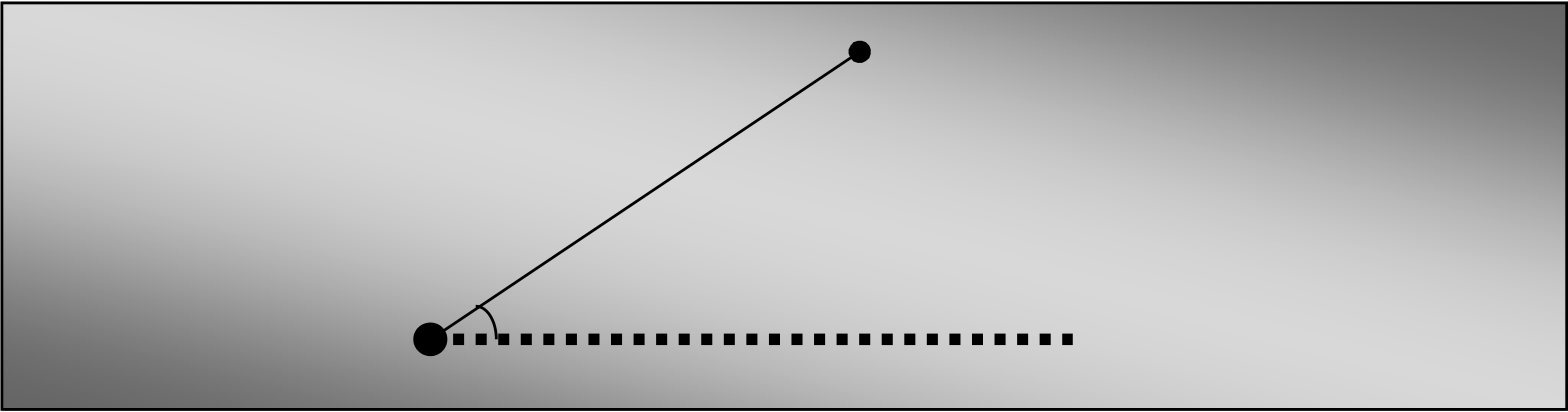
The angle of elevation θ to the object is shown below:

Object

Observer		horizontal

Observer		horizontal

Object

We very often see these notions in 3D shapes. For example,

	Bˆ AG

The angle of depression from H to C is the angle Fˆ HC (explain why!)

TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

Solution
(a) We consider the triangle AGB.

By Pythagoras’ theorem,

=36.9o

(b) For point F we consider the vertical height FC and thus the triangle AFC.

. Hence,
3  CAF =25.1o
41

	TOPIC 3: GEOMETRY AND TRIGONOMETRY	Christos Nikolaidis

30	45	horizontal

The angle of elevation from A is 45o.

The angle of elevation from B is 30o.

30°						45°
B			10		A	x
10x h 10						x			h 3				x		
10x h 10									h 3				x		
Therefore,		10 	h( 3 	1) =10 			h		10 3	1				13.7
h 3 =	h 	10 	h( 3 	1) =10 			h		10 3	1				13.7
Notice: Another approach is to work in triangle ABP first, to find AP=19.318 and then by sin 45 