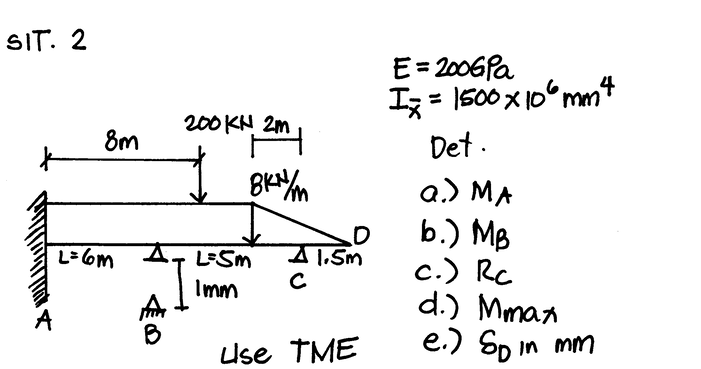
Mmax and delta dquestionstructural theoryuse three moment equation sit
Answer
Solved Step by step with explanation: Tp determine value of Ma, Mb, Rc ,Mmax and Delta d
RA + RB - 200 kN = 0 --(1)
Taking moments of point A:
To calculate the moments at points A and B, we can use the three-moment equation:
MA = (w1L1^2) / 2 - (w2L2^2) / 2 + Mmax
L1 = 8 m
L2 = 2 m
MA = 800 kNm - 200 kNm + Mmax
MA = 600 kNm + Mmax
To calculate Mmax, we need to find the point where the bending moment changes sign. This occurs at the point where the shear force changes sign. The shear force changes sign at point B.
Setting the shear force equation at point B to zero:
6RB = 1360 kN
RB = 226.67 kN
Mmax = 1133.33 kNm
Step 5: Calculate the reactions at the supports.
Step 6: Calculate the deflection at point C (Rc)
To calculate the deflection at point C (Rc), we need to determine the moment at that point. The moment at C can be calculated using the
MC = 800 kNm - 200 kNm + 1133.33 kNm
MC = 1733.33 kNm
The deflection at point C (Rc) can be calculated using the following equation:
Rc = MC / (E * Iz)
The maximum deflection (S0) can be determined by considering the beam's length and the maximum bending moment (Mmax). The formula for maximum deflection due to a concentrated load at the center of a simply supported beam is:
S0 = (5 * Mmax * L^2) / (384 * E * Iz)
a) MA = 600 kNm + Mmax
b) MB = 600 kNm - Mmax





