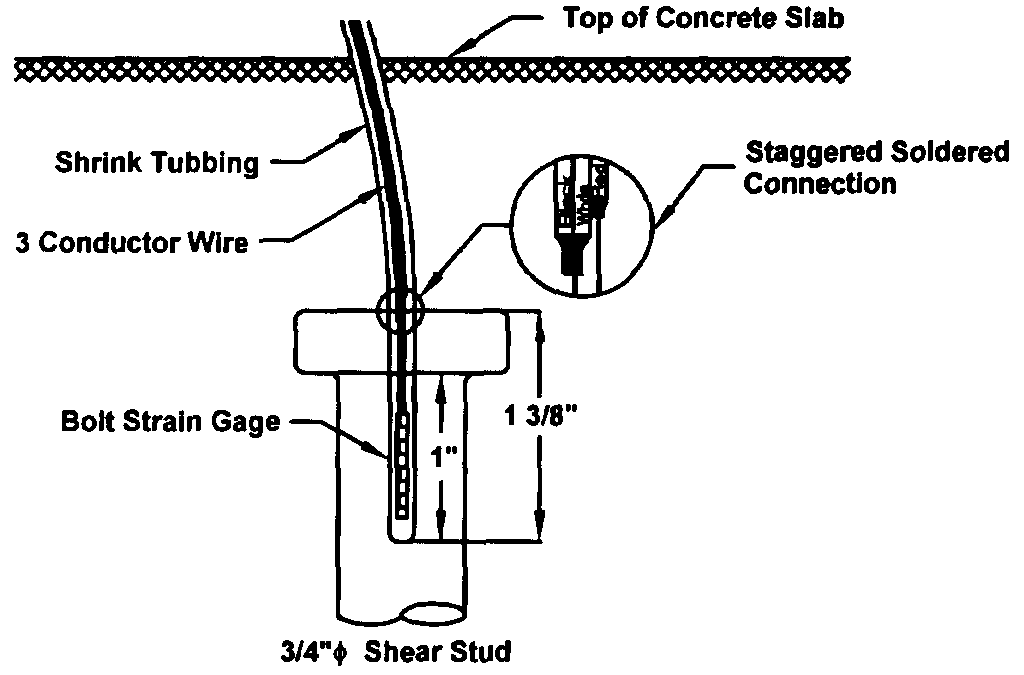
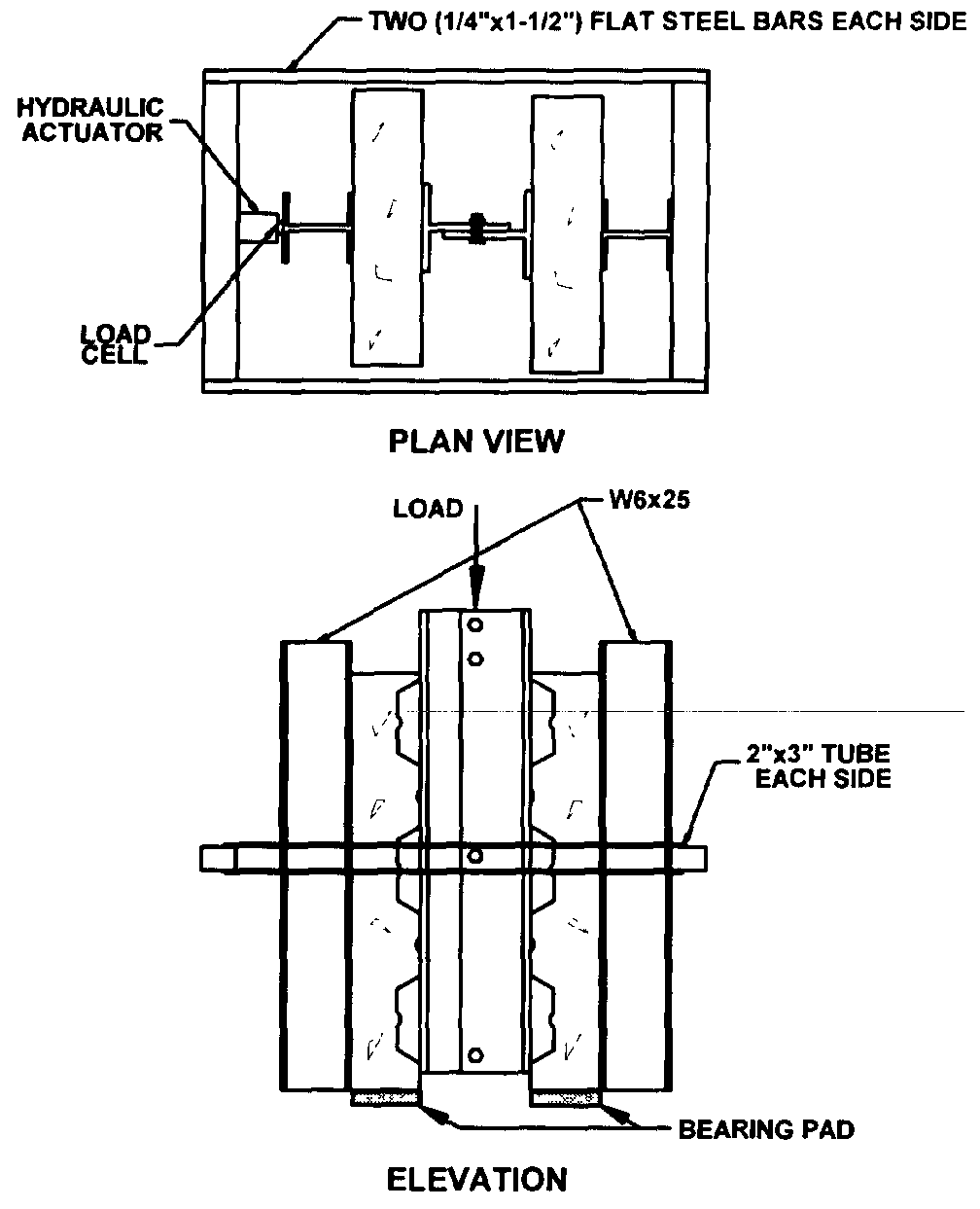
Load cell and hydraulic ram werepart the yoke assembly
Strength of Shear Studs in Steel Deck on Composite Beams and Joists
Q n = 05. A sc f c ' E c ≤A F sc u (1)
where
Ec = modulus of elasticity of concrete
Fu = minimum specified tensile stress of the stud shear connectorThis equation was developed based on results from elemental push-out tests.4 The stud reduction factor is given by:
| SRF | = | 085 | | w | r | | | H | s | − | 10 ≤ |
(2) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | r | h r | h r | |||||||||||
These equations, or similar forms, have been used in several design specifications, both in the United States and abroad. However, in recent years several researchers6-11 have shown that Equation 2 is unconservative for certain configurations. The studies have considered numerous parameters, including depth of steel deck shear stud height, concrete unit weight, position of shear stud in the deck rib relative to the bottom flange stiffener, number of shear studs in a given deck rib, and the amount and position of reinforcement in the slab. The studies reported results from push-out tests alone6,10,11 or a combination of push-out tests and beam tests.7-9 A conclusion common to all of the studies is that a modified, or completely different, stud reduction factor is needed. Modified calculation procedures have been developed and reported in the recent research studies. However, none of the studies have reported reasons for the discrepancy between the experimental data and Equations 1 and 2.
The reason for the discrepancy between recent experimental results with those predicted using Equations 1 and 2 is not clear. However, it is clear that a significant base of data exists to substantiate the procedures.3,12,13 A proper resolution of this dilemma will require careful consideration of all the data.
Test results were compared to calculated strength and stiffness values. The calculated shear stud strengths were determined using the LRFD Specification Equations 15-1 and 13-1 (Equations 1 and 2 in this paper). The flexural strength calculations were made using the equations given in the Commentary to the LRFD Specification. The elastic stiffness values were calculated using the lower bound moment of inertia defined in Part 4 of the LRFD Manual. Measured material properties were used in all calculations. The steel section properties that were measured (depth, flange thickness, flange width, and web thickness) were nearly identical to the tabular values given in Part 1 of the LRFD Manual. Therefore, tabulated cross-section properties for the steel shape were used in the calculations.
The flexural strength calculation procedure gives three equations for the nominal moment capacity, with the governing one determined based on the location of the plastic neutral axis (PNA). Yield stresses were determined separately for the web and flanges, thus the hybrid section idealization was used. All the specimens in this study were designed approximately 40 percent composite and the PNA was located in the web for all tests. The calculated moment capacity, Mc, using Equation C-I3-5,2 is given by:
| M | = | M | − | | C | | 2 | M | + | (3) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | p | | P yw | | pw |
| I= I+ A Y | − | d |
|
| ∑ | Qn | | d | + | Y | 2 | + |
|
) | 2 | (6) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | | F y | | ENA | |||||||||||||
TEST PROGRAM
where Beam Test Specimens
e = distance from center of steel section to the center
of the compressive stress block in the slab
| C | = | min | A | sw | F yw | + | 2 | (4) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | c | ' Ac | ||||||||||
| ∑ | ||||||||||||
where
Asw = area of steel web
The distance e is given by:
e = 0.5d + hr + tc – 0.5a (5)
stud nearest the support was placed in the strong position and the stud placement was alternated toward midspan. This resulted in a symmetric stud pattern in the two half-spans. (Test 4 was a repeat of the configuration used in Test 3 and was conducted due to the low concrete strengths obtained in Test 3.) The ribs in which shear studs were placed are shown in Figure 4. Note that all of the studs appear in the center of the deck ribs in Figure 4, however the studs were placed as described above.
The concrete slabs were formed using 6-in. cold-formed pour-stop material, resulting in three inches of cover on the 3-in. steel deck. A detail of the deck and slab is shown in Figure 5. After the concrete was placed, the slab was covered with plastic and cured for seven days. During this curing time the slab was kept moist. After seven days, the plastic and the pour-stop on the sides of the specimen were removed and the slab was allowed to cure for at least 21 additional days prior to testing. Concrete cylinders (4 in. × 8 in.) were cast at the same time as the concrete slab. The cylinders were kept adjacent to the slab, thus were covered with plastic and kept moist for the initial seven days.
Fig. 3. Composite deck profile.
End rotations were measured using two different techniques. Transducers were used to measure the upward deflection of the ends of the specimen and the support beam.
The 1 ft overhang was assumed to rotate rigidly about the
SECOND QUARTER / 1993 47
© 2003 by American Institute of Steel Construction, Inc. All rights reserved. This publication or any part thereof must not be reproduced in any form without the written permission of the publisher.
Fig. 7. Slip measurement detail.
A four-point loading system was used for all tests, with the loads spaced seven feet apart. The load was applied with a single hydraulic ram and distributed to the slab by a two-tier distribution system, as shown in Figure 9.
The load program was similar for all tests. An initial load, equal to approximately 15 percent of the calculated strength, was applied to seat the specimen and was then removed. The instrumentation was then re-initialized. Load increments were applied to the specimen until the load vs. centerline displacement response became non-linear. The specimen was then unloaded and then reloaded to the previous peak in three, approximately equal, increments. Displacement increments, based on the mid-span vertical deflection, were subsequently used to complete the test. The specimen was unloaded during the displacement controlled
phase if it was necessary to adjust the loading apparatus.
Push-Out Test Specimens
Push-Out Load Apparatus and Test Procedure
To prevent premature separation between the slab and steel deck, in a direction normal to the slab surface, a yoke device was placed on the specimen. This manner of loading simulated the gravity load placed on a slab in a composite beam/slab arrangement. A load cell and hydraulic ram were
Standard material tests were conducted on the concrete and steel components. The concrete cylinders were tested to determine compressive strength on the days of the various beam and push-out tests. Tensile coupons (0.5 in. width, 2 in. gage) were cut and machined from both the web and one flange of each structural steel shape, as well as from flat widths of the steel deck profile. The ultimate tensile stress for
TEST RESULTS
Beam Test Results
Fig. 11. Normalized midspan moment versus
displacement for composite beam specimens.
exhibited failure by developing concrete shear cones or by shearing off in the shank. Weak position studs exhibited failure by punching through the deck rib without developing a significant shear cone in the concrete or shearing in the stud shank. In Tests 1, 3 and 4, one or two of the strong position studs closest to one of the specimen supports sheared off in the shank. However, the weak position stud between the two strong position studs in Tests 3 and 4 did not shear off, but punched through the deck web and remained attached to the beam.
Push-Out Test Results
Table 2. Experimental and Calculated Results |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Test |
|
Me (ft-kips) |
Qcb/Qc | Qpo/Qc | Qcb/Qpo | Me/Mc | Me/Mpo | ||||
| 1 (str.) 2 (weak) 3 (alt.) 4 (alt.) |
|
|
|
||||||||
|
|||||||||||
The values Qc given in Table 2 are calculated stud strengths. These were determined using Equations 1 and 2 with measured material properties. Stud strengths Qcb, were back-calculated using the experimental moment from the beam tests, measured material properties and the calculation procedure described previously.
Because the shear studs in the weak position, in both the push-out and beam tests, failed by punching through the web of the deck it was hypothesized that their strength was not
position shear studs for push-out tests.
SECOND QUARTER / 1993 51
where fc' is the concrete compressive strength for the composite beam test, 18.82 kips is the average stud strength from the push-out tests, and 4.57 ksi is the concrete compressive strength from the push-out tests. The Qpo values represent stud strengths for the beam tests based on push-out test results.
axis for composite beam specimens.
Table 3. |
||||
|---|---|---|---|---|
| Test |
|
|||
|
||||
|
||||
Additionally, while a comparison between strong and weak position shear stud strengths indicates some difference, the more pronounced and significant difference is between the predicted values and the beam and push-out test results. The ratios Qcb / Qc or Qpo / Qc indicate the strong position values are approximately 70 percent of the predicted and the weak position values are approximately 60 percent of predicted.
The implications of the study described here, as well as previous studies, on composite beam design merit
52 ENGINEERING JOURNAL / AMERICAN INSTITUTE OF STEEL CONSTRUCTION
3.Use 50 percent composite action as a minimum, i.e., keep ΣQn/AsFy greater than or equal to 0.50. This will minimize the adverse effect of under-strength studs on the design moment strength, as reflected by the trend of the curves in Figure 2.
The result of implementing the above recommendations is an increase in the number of shear studs for designs utilizing one stud per rib. This will obviously result in a small increase in the cost, however the percentage increase in the in-place cost of the composite beam for these situations will be minor. Certainly in view of the questions that have been raised regarding the strength of the studs, the increase is warranted.
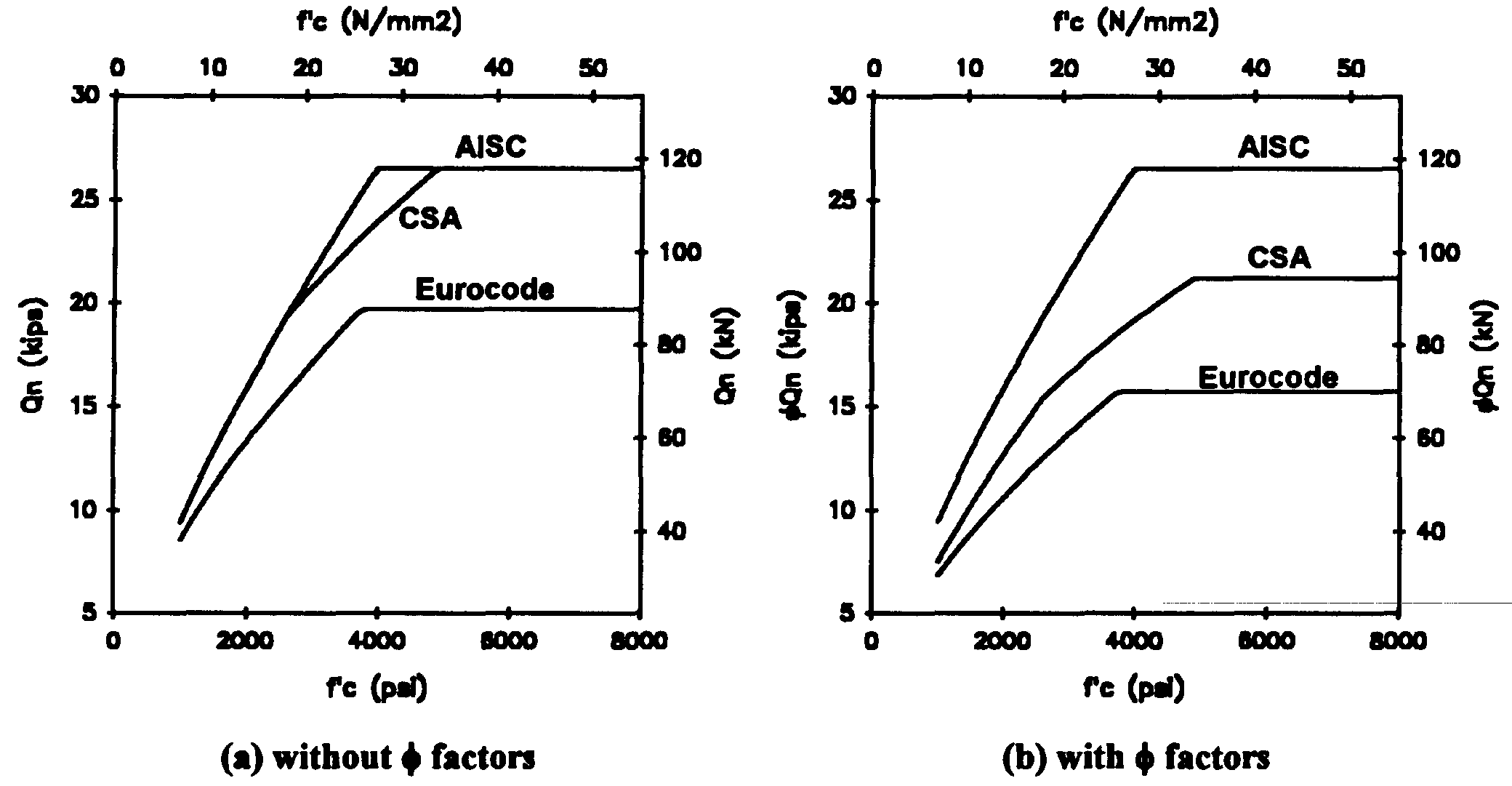
Fig. 14. Shear strength comparison for AISC, CSA, and Eurocode specifications.
ACKNOWLEDGMENTS
Graduate research assistant support for the project was provided by the American Institute of Steel Construction. The following organizations generously supplied material and equipment for the project: Virginia-Carolinas Structural Steel Fabricators Association (structural steel), Vulcraft Division of Nucor (steel deck pour-stop and welded wire fabric), and Nelson Stud Welding Division of TRW (shear studs and stud welding equipment). The remaining project costs were provided by Virginia Tech. The project from which the push-out test results were taken was sponsored by Nucor Research and Development.
3. Grant, J. A., Fisher, J. W. and Slutter, R. G, "Composite Beams with Formed Steel Deck," Engineering Journal, AISC, 14(1), 1977, pp. 24-43.
4. Ollgaard, J. G., Slutter, R. G. and Fisher, J. W., "Shear Strength of Stud Connectors in Lightweight and Normal Weight Concrete," Engineering Journal, AISC, 8(2), 1971, pp. 55-64.
Composite Beams: Push-out Tests," Canadian Journal of Civil
Engineering, 15, 1988, pp. 240-253.
12. Henderson, W. D., "Effects of Stud Height on Shear Connector Strength in Composite Beams with Light-weight Concrete in Three-Inch Metal Deck," Master of Science Thesis, The University of Texas, Austin, TX, 1976.
13. Klyce, D. C., "Shear Connector Spacing in Composite Members with Formed Steel Deck," Master of Science Thesis, Lehigh University, Bethlehem, PA, 1988.
Common Unified Rules for Composite Steel and Concrete Structures, Rep. EUR 9886, 1992.
18. Canadian Standards Association, Limit States Design of Steel Structures, CAN/CSA-S16.1-M89, Rexdale, Ontario, 1989.
a = depth of compression stress block
C = compressive force in concrete slab
© 2003 by American Institute of Steel Construction, Inc. All rights reserved. This publication or any part thereof must not be reproduced in any form without the written permission of the publisher.
|
|---|
Mfc = fully composite moment strength Mn = nominal moment strength
Pyw = web yield force
Qc = calculated stud strength using Equations 1 and 2
wr = average width of concrete rib
Ycon = distance from top of steel beam to top of concrete
© 2003 by American Institute of Steel Construction, Inc. All rights reserved. This publication or any part thereof must not be reproduced in any form without the written permission of the publisher.