All kinds of document library
ANTRIAN
Jika permintaan terhadap suatu jasa melebihi suplai, akan mengakibatkan terjadi antrian. Masalah tersebut dapat terjadi pada berbagai keadaan. Sebagai contoh Kendaraan menunggu lampu lalu lintas, para penumpang menunggu bis, para pelanggan menunggu di kasir bank, pesawat terbang menunggu ijin terbang, dan proses produksi menunggu bahan baku. Dalam jangka panjang kemacetan akan menyebabkan penumpukan yang akan mengakibatkan pemborosan biaya baik untuk bisnis maupun perorangan yang menunggu pada antrian.
Pasar swalayan berkepentingan dengan adanya antrian yang panjang, suatu pemecahan misalnya adalah menambah kasir. Cara ini akan mengurangi waktu pelanggan untuk menunggu. Akan tetapi menambah kasir akan menambah biaya pada pasar swalayan tersebut karena adanya penambahan kasir, ruangan dan peralatan. Model antrian akan sangat berguna untuk menentukan kapasitas optimal dari suatu fasilitas.
Sistem antrian terdiri dari beberapa komponen dasar. Unit yang memasuki sistem disebut pelanggan dan dikatakan datang dari sumber kedatangan atau sumber populasi. Pelanggan dalam antrian dilayani menurut aturan yang ada yaitu disiplin antrian atau disiplin pelayanan. Pelayanan diberikan oleh mekanisme pelayanan atau fasilitas pelayanan. Pelanggan yang telah menerima pelayanan meninggalkan sistem, seperti terlihat pada gambar 1.
Pelanggan Pelanggan
dalam antrian meninggalkan antrian Sumber kedatangan Fasilitas
pelayanan
Gambar 1 : sebuah sistem antrian
UNIT 8 – TEORI ANTRIAN
Seluruh komponen pada sistem pelayanan mempunyai sifat-sifat yang spesifik.
Sumber kedatangan dapat berupa tak terbatas maupun terbatas. Jika ukuran dari sumber kedatangan sangat besar dan tidak mudah diidentifikasi kita katakan sebagai tak terbatas. Namun jika sumber kedatangan kecil, mudah diidentifikasi dan dapat dihitung dengan tepat, Jika kedatangan seorang pelanggan mengubah besar kemungkinan kedatangan pelanggan lainnya, sumber kedatangan dapat diartikan sebagai terbatas.
Proses kedatangan digambarkan sebagai tingkat kedatangan dapat secara acak, ataupun deterministik. Pembahasan pada antrian di sini difokuskan pada kedatangan yang acak.
Terdapat berbagai jenis antrian yang dapat terjadi, a.l. Yang pertama kali datang lebih dahulu dilayani / First come first served (FCFS), Yang terakhir kali datang lebih dahulu dilayani / last come first served (LCFS), pelayanan dengan urutan secara acak / service in random order (SIRO), dan lain sebagainya. Pembahasan difokuskan pada disiplin antrian first come first served.
Proses pelayanan digambarkan sebagai tingkat penyelesaian pelayanan. Walaupun waktu pelayanan yang tetap adalah memungkinkan, namun dalam pembahasan difokuskan pada waktu penyelesaian yang acak.
Untuk situasi antrian yang diberikan, Kita mungkin ingin mencari pemecahan persoalan beberapa hal sebagai berikut:
1. Berapakah waktu rata-rata dari setiap pelanggan berada dalam sistem (waktu tunggu ditambah waktu pelayanan)?.2. Berapakah jumlah rata-rata pelanggan dalam sistem?
3. Berapakah jumlah rata-rata pelanggan yang berada dalam antrian?
4. Berapakah waktu rata-rata yang dikeluarkan setiap pelanggan dalam antrian? 5. Berapakah besar kemungkinan pelanggan yang datang menemukan fasilitas pelayanan dalam keadaan menganggur?
6. Berapakah besar kemungkinan pelanggan yang datang menemukan telah ada sejumlah tertentu pelanggan berada dalam sistem?
Pemecahan yang diberikan untuk permasalahan tersebut bersama dengan perkiraan biaya pelayanan, pembatasan antrian pelanggan dan biaya tunggu dapat
2
UNIT 8 – TEORI ANTRIAN
dibuat keputusan yang optimal berdasarkan pelayanan yang diinginkan dan biaya pelayanan dari fasilitas.
Pada sistem antrian pada keadaan awal sistem antrian dalam keadaan transien dan akhirnya masuk ke dalam keadaan tunak (steady state). Pembahasan kita berikutnya adalah pada sistem dalam keadaan tunak.
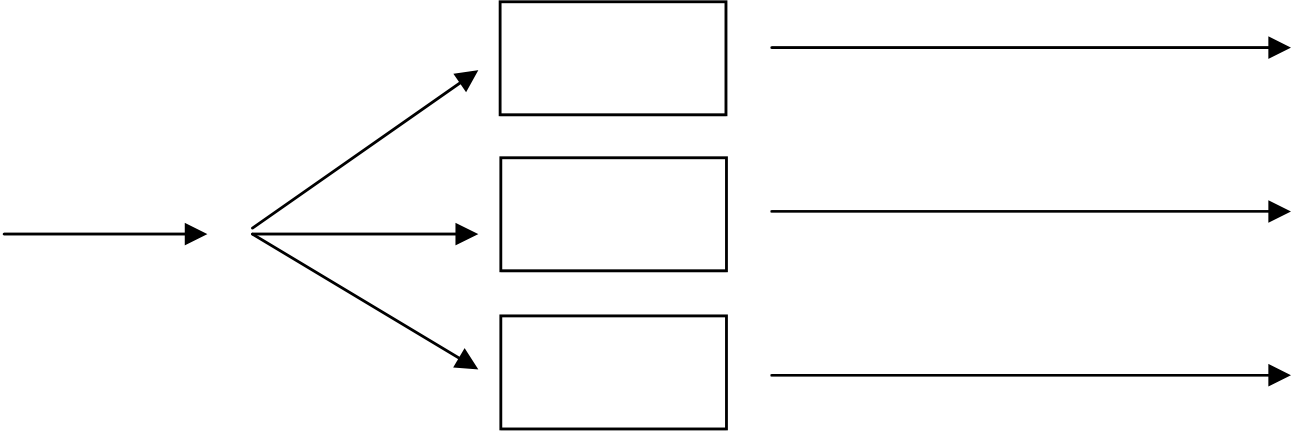
Terdapat berbagai konfigurasi antrian; yaitu fasilitas antrian tunggal pelayanan tunggal yang dapat dilihat pada gambar 1, fasilitas antrian tunggal pelayanan jamak, pada gambar 2, fasilitas antrian jamak pelayanan jamak pada gambar 3.
pelayanan
pelayanan
pelayanan
gambar 2 sistem antrian tunggal pelayanan jamak
pelayanan
pelayanan
pelayanan
gambar 3 sistem antrian jamak pelayanan jamak
3
UNIT 8 – TEORI ANTRIAN
DISTRIBUSI EKSPONENSIAL
Salah satu distribusi kemungkinan yang digunakan secara luas untuk waktu antar kedatangan (yaitu waktu antara dua kedatangan yang berturut-turut) adalah distribusi eksponensial. Diketahui untuk beberapa sistem antrian distribusi eksponensial dapat menyediakan data observasi aktual yang pas. Kita juga harus mempertimbangkan waktu pelayanan terdistribusi secara eksponensial.
Distribusi kemungkinan eksponensial didefinisikan sebagai variabel acak x yang kontinyu dengan parameter r dan dengan fungsi densitas kemungkinan f(x) yang dliberikan sebagai :
f(x) = r.e-rx (x > 0)
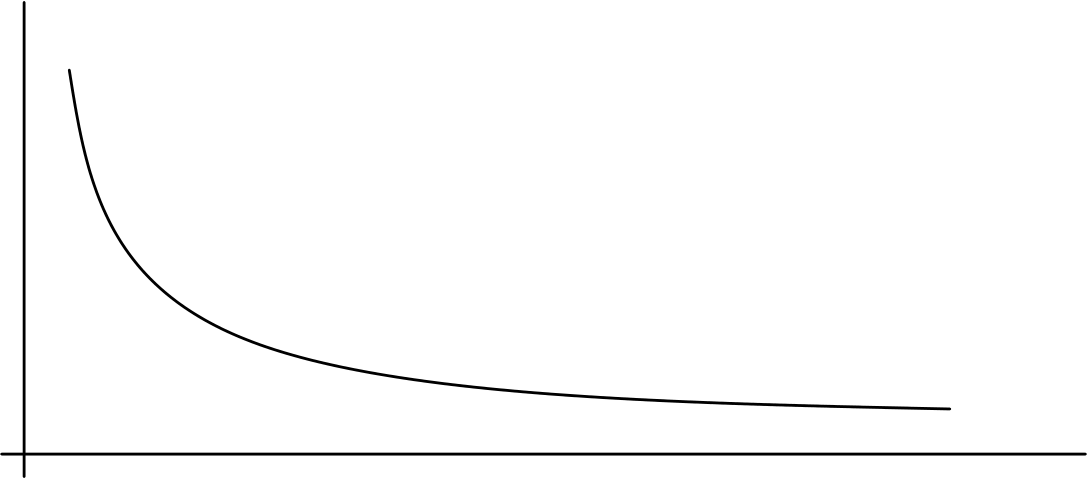
Hal tersebut ditunjukkan pada gambar 4
| f(x) |
|---|
x
gambar 4 distribusi eksponensialUntuk distribusi eksponensial dengan parameter r, nilai yang diharapkan E(x), diberikan sebagai berikut :
E(x) = 1/r
Variansi V(x), diberikan sebagai berikut :
V(x) = 1/r2
F(x), densitas fungsi kemungkinan kumulatif untuk distribusi eksponensial rumusnya sebagai berikut:
F(x) = 1 – e-rx (x > 0)
4
UNIT 8 – TEORI ANTRIAN
Contoh 1
Waktu rata-rata antara 2 panggilan telepon yang datang pada papan pembagi (switchboard) adalah 20 detik. Waktu tersebut terdistribusi secara eksponensial. Berapa kemungkinan waktu kedatangan antara 2 telepon adalah 0.5 menit.Penyelesaian :
Jika r adalah distribusi parameter, maka 1/r = 20 detik = 1/3 menit atau r = 3 panggilan/menit.Oleh karena itu P ( waktu kedatangan < 0.5 menit ) = P (x <0.5) = 1 - e -3 x 0.5 = 1 - 0.2231 = 0.7769
5
UNIT 8 – TEORI ANTRIAN
DISTRIBUSI POISSON
Distribusi Poisson memberikan kemungkinan/probabilitas jumlah kedatangan untuk setiap periode yang diberikan untuk bermacam proses yang ditemukan pada kehidupan nyata. Didefinisikan sebagai variabel acak Y dengan parameter dan dengan fungsi distribusi kemungkinan p(y) yang dirumuskan sebagai berikut:
| P(y) = P(Y=y) = | e | . |
|
|---|---|---|---|
| y ! |
Hal tersebut ditunjukkan pada gambar 5
P(y)
y
gambar 5 distribusi PoissonUntuk distribusi Poisson dengan parameter r, nilai yang diharapkan, E(y) dirumuskan sebagai :
E(Y) = r
Variansi V(Y), dirumuskan V(Y) = rContoh 2
Diambil dari contoh 1 jumlah telepon yang datang tiap menit terdistribusi secara Poisson r = 3 tiap menit. Hitung kemungkinan dari jumlah kedatangan telepon setiap menit adalah
a. 4
b. 2 atau lebih kecil
6
UNIT 8 – TEORI ANTRIAN
Penyelesaian :
a. P(Y=4) = e-3.34 / 4! = 0,0498 x 81 / 24 = 0.1681
b. P(Y=2) = P(Y = 0) + P(Y = 1) + P(Y = 2) = e-3.30 + e-3.31 + e-3 32
| 0! | 1! |
|
|---|
= 0.498 + 0.1494 + 0.2241 = 0.4233
7
UNIT 8 – TEORI ANTRIAN
MODEL ANTRIAN PELAYANAN TUNGGAL
Model antrian yang ada dibagian ini adalah masalah antrian yang mempunyai karakteristik sebagai berikut:
1. Antrian tunggal yang tidak terbatas
2. Jumlah kedatangan yang terdistribusi secara Poisson
3. Sumber kedatangan tidak terbatas
4. disiplin antrian adalah first come first serve
5. waktu pelayanan terdistribusi secara eksponensialNotasi yang digunakan pada model diatas:
λ = tingkat kedatangan pelanggan per periode waktu
μ = tingkat pelayanan rata-rata per periode waktu
ρ = λ / μ , Intensitas traffic (atau tingkat kegunaan), diasumsikan kurang dari 1 Pn = kemungkinan n pelanggan terdapat dalam sistem (antrian sedang dilayani), n= 0,1,2,3, . . . . .dengan menggunakan simbol diatas, didapat hasil sebagai berikut:
1. Probabilitas pada sistem yang menganggur, atau tidak ada langganan sama sekali pada sistem, Po adalah:
Po = 1 - = 1 - :
2. Probabilitas pada sistem yang tidak menganggur, oleh karena itu: P (n > 0) = ;
3. Rumus umum untuk probabilitas yang terdapat n unit (langganan) dalam sistem diberikan sebagai berikut:
|
| n |
|
|---|---|---|---|
| |
n = 0, 1, 2, 3 . . . .
8
UNIT 8 – TEORI ANTRIAN
4. Ls adalah jumlah pelanggan yang diharapkan berada dalam sistem (menunggu atau sedang dilayani), adalah:
| L | | | |
|
|||
|---|---|---|---|---|---|---|---|
| s | | | 1 | |
|
||
5. Ws adalah Waktu yang diharapkan untuk pelanggan yang datang berada dalam sistem ( dari saat datang, mengantri dan dilayani), adalah :
| W | | 1 | | L | s | |
|---|---|---|---|---|---|---|
| s | | | | |||
6. jika Lq adalah jumlah pelanggan yang diharapkan berada dalam antrian, dan Wq waktu yang diharapkan pelanggan berada dalam antrian, maka :
| W q | | | X | 1 | | | W | |
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| | | s |
|
|||||||||||
| L | | | X | | | W |
|
|||||||
| q | | | | |
|
|||||||||
Contoh 18.3
Tingkat kedatangan Pelanggan pada kantor pos rata-rata 8 orang per jam.Setiap pegawai kantor pos melayani pelanggan rata-rata 20 per jam.
a. Berapa probabilitas tidak ada pelanggan pada kantor pos (sistem menganggur) ? b. Berapa probabilitas yang ada lebih dari 2 pelanggan dalam kantor ?
c. Berapa probabilitas yang tidak ada pelanggan yang menunggu untuk dilayani ? d. Berapa probabilitas pelanggan yang sedang dilayani dan tidak ada yang menunggu ?
e. Hitunglah Ls, Lq, Ws, dan Wq
Penyelesaian:
Dengan = 8 per-jam dan = 20 per-jam, kita peroleh:
|
|
|
|
| 4,0 ) | X | 4,0 | n | | 6,0 | X | 4,0 | n |
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P n | | 1( | | ) | Xn | | 1( | ||||||||||||
9
UNIT 8 – TEORI ANTRIAN
a. P [tidak ada pelanggan di kantor) = Po = 1 – (2/5) = 3/5 = 0,6 b. P [lebih dari 2 pelanggan di kantor]
= l – P[pada lebih dari 2 pelanggan di kantor]
= 1 - [P0 + P1 + P2]
= 1 – [3/5 + 3/5 x 2/5 + 3/5 x (2/5 )2]
= 8/125 = 0,064
c. P[tidak ada pelanggan yang menunggu]
= p[pada lebih dari 1 pelanggan menunggu di kantor]
= [P0 + P1]
= 3/5 + 3/5 x 2/5 = 21/25 = 0,64
d. P[ada pelanggan sedang dilayani dan tidak seorang pun pelanggan yangmenunggu] = P1
= 3/5 x 2/5 = 6/25 = 0,24
| e. | L | | | | 8 |
|
|||
|---|---|---|---|---|---|---|---|---|---|
| s | - | | 20 | | 8 | ||||
(angka diatas adalah rata-rata jumlah pelanggan di kantor pos) ;
| W | L | s |
|
|---|---|---|---|
| s | | ||
(waktu diatas merupakan waktu rata - rata yang diperlukan oleh pelanggan di kantor pos)
| W q | W s | - |
|
|---|
(waktu diatas merupakan waktu tunggu yang diperlukan pelanggan dalam antrian)
Akhirnya Lq = Wq x = 8 x (2/60) = 4/15 - 0,267
(jumlah tersebut adalah Jumlah pelanggan yang menunggu untuk dilayani)Contoh 18.4
Sebuah perusahaan penerbangan memiliki satu petugas pemesanan tempat yang bertugas pada cabang lokal. Petugas menangani informasi pesanan tempat penumpang dan waktu penerbangan. Jumlah pelanggan yang datang selama periode waktu yang diberikan didistribusikan secara Poisson dengan tingkat kedatangan 8 per
10
UNIT 8 – TEORI ANTRIAN
jam, dan petugas pemesanan tempat dan melayani pelanggan dalam rata-rata 6 menit, dengan waktu pelayanan yang terdistribusi eksponensial.
a. Berapa probabilitas sistem yang sibuk?
b. Berapa rata-rata waktu yang dikeluarkan pelanggan dalam sistem dan dalam antrian?
c.Berapa rata-rata panjang antrian, dan berapa rata-rata jumlah pelanggan dalam sistem?
Pemecahannya :
dengan λ = 8 per jam dan = 10 per jam,
|
| 8 | 5 | ||
|---|---|---|---|---|---|
| |
|
4 |
maka,
a. P[sistem sedang sibuk] = P(n > 0) = 1 - Po = = 0,8
b. Waktu rata rata yang dihabiskan dalam sistem, Ws = adalah :
| W | | 1 | | 1 |
|
|||
|---|---|---|---|---|---|---|---|---|
| s | μ | | λ | 10- | 2 |
Kita juga dapat memperoleh jawaban yang sama dengan menggunakan hubungan di bawah ini :
|
W | - | 1 |
|
|---|---|---|---|---|
| q | s | |
c. Panjang antrian rata rata, Lq adalah
| L | | λ | x | λ |
|
||
|---|---|---|---|---|---|---|---|
| q | μ | μ | | λ |
Kita juga dapat memperoleh jawaban yang sama dengan menggunakan hubungan di bawah ini :
Lq = Wq x = 8 x (2/5) = 3,2 pelanggan
Rata-rata jumlah pelanggan dalam sistem, Ls adalah
| Ls |
|
|---|
11
UNIT 8 – TEORI ANTRIAN
Contoh 18.5
Andaikata manajemen perusahaan penerbangan memutuskan untuk menyewa satu atau lebih petugas pemesanan tempat untuk mengoperasikan dalam pararel dengan petugas yang ada (dua baris yang terpisah).a. Berapa probabilitas pada sistem yang sibuk, dua petugas sedang sibuk?
b . Berapa rata-rata waktu yang dikeluarkan pelanggan pada sistem dan dalam antrian?
c. Berapa rata-rata panjang antrian, dan berapa rata-rata jumlah pelanggan pada sistem?
Penyelesaian
Sistem dapat diilustrasikan dengan gambar 18.6
|
= 10 |
|---|
|
|---|
|
= 10 |
|---|
|
|---|
gambar 18.6 : 2 petugas dan 2 antrian
Karena ada 8 kedatangan per jam, tingkat kedatangan untuk tiap 2 antrian pada kantor adalah setengah jumlah total, = 4 untuk masing-masing antrian.
Dengan = 4 per jam dan = 10 per jam
| |
|
|---|
maka :
a. P[sistem sedang sibuk] = P[kedua petugas sibuk]
= (1 - Po) x (1 - Po) = (1 – (6/10)) x (1 – (6/10)) = 0,16
b. rata-rata waktu yang dihabiskan dalam sistem, Ws = adalah :
| Ws | | 1 |
|
||
|---|---|---|---|---|---|
| μ | | λ |
Rata-rata waktu yang dihabiskan dalam antrian, Wq menjadi :
12
UNIT 8 – TEORI ANTRIAN
| Wq | |
|
1 |
|
||
|---|---|---|---|---|---|---|
|
|
|
= 4 menit
c. Panjang antrian rata rata, Lq adalah
| L | | λ | X | λ |
|
||
|---|---|---|---|---|---|---|---|
| q | μ | μ | | λ |
= 0,267 pelanggan
Jumlah rata-rata pelanggan dalam setiap sistem, Ls adalah :
| Ls | |
|
|
|---|---|---|---|
| - | | ||
Kita akan membandingkan hasil perhitungan sistem antrian dengan dua sistem antrian lain pada bagian berikut.
13
UNIT 8 – TEORI ANTRIAN
MODEL ANTRIAN TUNGGAL PELAYANAN JAMAK
Terdapat banyak situasi dimana terdapat lebih dari satu pelayanan tetapi hanya terdapat satu antrian. Sebagai contoh, antrian tunggal pada antrian bank untuk pelayanan oleh berbagai kasir. Ini adalah sistem antrian tunggal dengan pelayanan jamak digambarkan pada gbr 18.2 yang lalu.
Model antrian ini dapat dipergunakan untuk seluruh masalah antrian yang memiliki karakter sebagai berikut :
a. terdapat antrian tunggal yang tak terbatas
b. jumlah kedatangan didistribusikan secara Poisson
c. calling population tak terbatas
d. disiplin antrian adalah pertama datang pertama yang dilayani
e. Terdapat beberapa pelayanan, dan pelanggan yang terdepan pada antrian akan dilayani segera setelah terdapat loket/pelayan yang kosong
f. semua loket/pelayanan mempunyai tingkat pelayanan yang sama dan waktu pelayanan terdistribusi secara eksponensial.Kita sekarang harus menggambarkan beberapa persamaan matematik yang telah dikembangkan untuk menganalisa model antrian tunggal dengan pelayanan jamak. Kita mengasumsikan adanya sejumlah c fasilitas pelayanan masing-masing tingkat pelayanan adalah dan adalah kurang dari c.
Kita lalu mempunyai hasil sebagai berikut :
1. Probabilitas pada sistem dalam keadaan mengganggur, yaitu tidak ada pelanggan
|
|
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| P | | 1 | |||||||||
| o | c1 |
| | | |||||||
|
i ! | c 1(! | |
|
|||||||
14
UNIT 8 – TEORI ANTRIAN
untuk c = 3
| P | |
|
| 1 | 3 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| o | 2 |
| | 3 | 0 | | | | 2 | | |||||||||
|
i ! | 1(!3 | |
|
!0 | !1 | !2 | 1(!3 | |
|
|||||||||
2. Probabilitas bahwa terdapat n pelanggan pada sistem, P diberikan oleh:
| P | | P | x |
|
|
|||
|---|---|---|---|---|---|---|---|---|
| n | o |
|
||||||
| P | | P | x | n |
|
|||
| n | o | c ! | nc | | c | |||
Terdapat dua ekspresi berbeda Pn untuk n < c, beberapa pelayanan mengarggur, dan sistem tidak digunakan sepenuhnya pada kapasitas pelayanan.
3. Lq adalah jumlah pelanggan yang diharapkan dalam antrian, sbb :
| L | | P | x | | 1 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q | o | c( | | 1 )! | x (c | - | ) | 2 | ||||
4. Ls adalah jumlah pelanggan yang diharapkan pada sistem, sbb :
Ls = Lq +
5. Wq adalah waktu yang diharapkan untuk pelanggan berada dalam antrian dan oleh WS waktu yang diharapkan pelanggan berada pada sistem. sbb :
| W | L | q |
|
W | | L | s | | L | q | | 1 | | W | |
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q | | s | | | | q |
|
|||||||||
Contoh 18.6
Untuk mendaftar pada Universitas Concordia, mahasiswa harus datang pada kasir kantor untuk membayar uang kuliah mereka. Rata-ratanya, 5 mahasiswa datang pada kasir setiap menit. Terdapat 2 kasir yang bekerja sepanjang waktu dan masing-masing rata rata dapat melayani 3 orang mahasiswa per menit. Mahasiswa mengantri dalam bentuk antrian tunggal dikantor untuk membayar uang kuliah mereka. Mahasiswa yang ada dibarisan terdepan akan datang pada kasir yang kosong. a. Berapa probabilitas pada sistem yang menganggur?b. Berapa probabilitas paling sedikit satu mahasiswa menunggu untuk dilayani? c. Berapa rata-rata jumlah mahasiswa di kantor kasir?
d. Berapa rata-rata waktu untuk menunggu bagi seorang mahasiswa?
15
UNIT 8 – TEORI ANTRIAN
Pemecahannya:
dengan = 5 per menit, = 3 per menit dan c = 2 pelayanan, kita lihat bahwa 5<2x3, bahwa <c<, = 5/3
maka,
| a. | P | |
|
P | | 1 | 3 ) |
|
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| o | 1 | | | 2 | o | 1 | | 5 | | ( 5 | / | 2 | ||||||||||
| 1(!2 | |
|
3 | 1(!2 | | ( 5 | / | 3 ) | ) | |||||||||||||
|
2 | |||||||||||||||||||||
P0 Merupakan nilai probabilitas sistem sedang tidak bekerja.
b.P[saat setidak-tidaknya 1 orang menunggu]
= 1 - P[tidak seorang mahasiswapun yang menunggu]
= 1 - [P0 + P1+ P2]
Selama ada tidak lebih dari 2 orang mahasiswa yang menunggu di kantor kasir, maka tidak akan ada antrian.
| Dengan | P | | P 0 | x | 1 |
|
|||
|---|---|---|---|---|---|---|---|---|---|
| 1 | !1 | ||||||||
| P 2 | | P 0 | x | 2 |
|
||||
| !2 | |||||||||
diperoleh 1 – [P0 + P1 + P2] = 1 – 1/11x5/3 – 1/11x(5/3)2 = 1 - [1/11 + 5/33 + 25/198] = 1 – (73/198) = 125/198 = 0,6313
c.Jumlah mahasiswa rata-rata pada kantor kasir, Ls diperoleh :
| L | | P o | x | |
|
| | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s | c( | | 1 )! | x (c | - | ) | 2 | ( | 5 | / | 3 | ) | | 60 | ||||||||||||||
| L |
|
1 | x | ( | 5 | / | 3 | ) | 2 | 3 | )) | | ||||||||||||||||
| s | 11 | !1 | x | (2 | - | ( | 5 | / | 2 | 11 | ||||||||||||||||||
= 5,4545 mahasiswa
16
UNIT 8 – TEORI ANTRIAN
d.rata-rata waktu tunggu untuk setiap mahasiswa. Wq menjadi :
| W | | L | s | | 1 |
|
|---|---|---|---|---|---|---|
| q | | | ||||
Perusahaan penerbangan (contoh 18.4) mempunyai dua petugas pemesanan tempat yang melayani penumpang yang antri dalam bentuk tunggal di kantor. Jika jumlah kedatangan pelanggan adalah 8 per jam dan tiap petugas dan melayani setiap pelanggan dalam 6 menit, lalu :
a. Berapa probabilitas sistem sibuk, yang kedua petugasnya sedang sibuk?b. Berapa rata-rata waktu yang dikeluarkan seorang pelanggan pada sistem, dan pada antrian?
c. Berapa rata-rata panjang antrian, dan berapa rata-rata jumlah pelanggan pada sistem.
Pemecahannya :
Situasi ini dapat diilustrasikan pada gambar 18.2
dengan = 8 per jam, = 10 per jam dan c = 2 pelayanan, kita memiliki 8 < 10x2 sebagai contoh < x c, = 8/10
| P | |
|
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| o | 1 | | | 2 |
|
|||||||||||||
| 1(!2 | | |||||||||||||||||
| P | |
|
||||||||||||||||
| 1 | ||||||||||||||||||
| o | 1 | | 8 | / | 10 | | ( 8 | / | 10 ) |
|
||||||||
| 1(!2 | | ( 8 | / | 10 ) | ) | |||||||||||||
|
||||||||||||||||||
a.P[sistem sedang sibuk] = 1 - [P0 + P1]
= 1 – [P0 + P1 x (1/(1!))
= 1 – (3/7 + (3/7 x 8/10)) = 8/35 = 0,229
b.Waktu rata-rata yang dihabiskan oleh pelanggan di dalam sistem, Ws di dapat :
| W | | L | q | |
|
|---|---|---|---|---|---|
| s | |
|
|||
17
UNIT 8 – TEORI ANTRIAN
dimana nilai Lq adalah :
| L | | P o | x | |
|
|||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s | c( | | 1 )! | x (c | - | ) |
|
| 16 | 105 |
|
|||||||||||||
| L | | 3 | / |
!1 |
( 8 | / | 10 ) |
|
||||||||||||||||
| s | x (2 | - | ( 8 | / | 10 )) | 2 | ||||||||||||||||||
oleh karena itu :
Wq = Lq/λ = 16/105/8 = 0,019 jam = 1,14
| W | | L | q | |
|
||
|---|---|---|---|---|---|---|---|
| s | |
|
|||||
c.Panjang rata-rata dari antrian, Lq diberikan :
| L | 16 |
|
|---|---|---|
| q | 105 |
Jumlah rata-rata pelanggan dalam sistem, Ls diberikan dari : Ls = Lq +
= 16/105 + 8/10
= 100/105 = 0,952 pelangganKita sekarang membandingkan hasil yang diperoleh pada contoh 18.4, 18.5 dan 18.7. Ini dirunjukkan pada tabel 18.1. Catatan yang pada sistem dua pelayanan dua antrian, karena terdapat dua antrian pararel, Ls dan Lq untuk masing-masing antrian (0,67 dan 0,27) yang telah digandakan.
Dari tabel 18.1, kita melihat sebagai berikut :
1.Jumlah orang pada sistem berkurang ketika dua pelayanan ditugaskan untuk melakukan suatu pekerjaan.2.Jumlah orang yang menunggu dalam antrian lebih banyak menurun pada kasus antrian tunggal, dua sistem pelayanan, dan peningkatan lebih dari dua antrian.
Kita dapat menyimpulkan bahwa antrian tunggal, dua sistem pelayanan lebih efesien.
18
UNIT 8 – TEORI ANTRIAN
3.Waktu menunggu pada antrian menurun dari 24 menit untuk antrian tunggal, sistem pelayanan tunggal menjadi 4 menit untuk antrian jamak, sistem pelayanan jamak. Dan menurun melebihi 1,3 menit untuk antrian tunggal, sistem pelayanan jamak. Kecerendungan yang sama juga dapat ditunjukkan untuk waktu total yang dihabiskan dalam sistem.
|
|
|
|
|---|---|---|---|
| LS | 4 | 2 x 0,667 = 1,334 | 0,952 |
| LQ | 3,2 | 2 x 0,267 = 0,534 | 0,152 |
| WS | 30 menit | 10 menit | 7,14 menit |
| WQ | 24 menit | 4 menit | 1,14 menit |
19
UNIT 8 – TEORI ANTRIAN
MODEL-MODEL ANTRIAN POPULASI BERHINGGA
Pada banyak situasi kehidupan yang nyata sumber kedatangan/calling source adalah berhingga. Sebagai contoh beberapa terminal komputer yang datang untuk direparasi pada bagian servis komputer terbatas. Pada keadaan seperti ini jumlah dari unit yang ada dalam sistem (di bagian servis), akan memberikan pengaruh pada nilai kemungkinan kedatangan bagi pengunjung baru. Sebagai contoh jika semua bagian servis sedang melakukan aktivitas reparasi, maka tidak akan ada lagi pengunjung.
Kita dapat mengasumsikan bahwa setiap terminal memiliki waktu yang terdistribusi secara eksponensial antara neninggalkan sistem, pembaruan reparasi, rusak pada waktu berikutnya dan memasuki sistem antrian lagi.
Jika m adalah jumlah unit dari populasi yang berhingga, dan adalah rasio dari kedatangan dari setiap unit populasi.
Rasio kedatangan efektif dapat didenifisikan sebagai rasio kedatangan individu dikalikan dengan jumlah unit dalam populasi yang tidak termasuk dalam sistem antrian. Dengan kata lain : x (m – LS)
Dimana m-LS merupakan jumlah rata-rata dari unit yang tidak termasuk dalam sistem antrian. Sebagai contoh, jika jumlah total dari terminal adalah 20, dengan nilai rata-rata dari dua kerusakan per terminal dalam satu 1 hari, kemudian ratio efektif kedatangan (diberikan sebagai nilai rata-rata sebesar 5 terminal dalam sistem) adalah x (m – LS) = 2 x(20-5) = 30
Sebagai catatan nilai ρ dapat lebih besar dari 1, oleh karena panjang maksimum dari antrian adalah m-1, dan tidak akan ada antrian tak berhingga yang terjadi. Dengan menggunakan simbol standard, kita memiliki formulasi dibawah ini untuk populasi terbatas, model pelayanan antrian tunggal :
1.Nilai probabilitas jika sistem menganggur, Po diberikan sebagai berikut :
| Po | | 1 | |
|---|---|---|---|
m i0 |
(m - i) ! |
20