Four – point dft two-point dft
Chapter 10 The Discrete Fourier Transform and
Fast Fourier Transform Algorithms
10-1 Introduction
1. x(t) --- Continuous-time signal
(1) Sample x(t) =>
x0, x1, … , xN-1 over T (for example 1000 seconds)
(2) Discrete Fourier Transform (DFT):
=> $X_{k} = \sum_{n = 0}^{N - 1}{x_{n}e^{- j2\pi\frac{\text{kn}}{N}}\begin{matrix} & & & k = 1,2,\text{.}\text{.}\text{.},N \\ \end{matrix}}$
$0 \leq \omega < 2\frac{\pi N}{T}$
4. $x_{n} = \frac{1}{N}\sum_{k = 0}^{N - 1}{X_{k}e^{j2\pi\frac{\text{kn}}{N}}}$ ---- periodic function (period N)
$X_{k} = \sum_{n = 0}^{N - 1}{x_{n}e^{- j2\pi\frac{\text{kn}}{N}}}$ period function (period N)
10-2 Error Sources in the DFT
$\Pi(\frac{t - t_{0}}{Tunderbracealignl\underset{\text{width}}{\overset{\begin{matrix} \uparrow \\ \end{matrix}}{\underbrace{}}}\text{of}}\text{the}\text{window}) \leftrightarrow T\text{sin}c(\text{Tf})e^{- j2{\pi t}_{0}f}$ $\begin{matrix} \text{sin}\text{cX} = \frac{\text{sin}\pi x}{\pi x} \\ \Rightarrow \text{sin}c(\text{Tf}) = \frac{\text{sin}\pi\text{Tf}}{\pi\text{Tf}} \\ \end{matrix}$
when t0 = 0 $\Pi(\frac{t}{T}) \leftrightarrow T\text{sin}c(\text{Tf})$
Its Fourier transform
$X(f) = \frac{2\pi}{1 + (2\pi f\tau)^{2}}$
periodic function, introduce frequencies beyond fs .
Limited T (over which x(t) is sampled to collect data for DFT)
Effect of limited T
(3) Dose DFT give Xsω(f) for every f ?
use $\Pi(\frac{t}{4})$ for $e^{- \frac{|t|}{\tau}}$
Effect of T (window size)
Aliasing
$X_{s}(f) = f_{s}\sum_{n = - \infty}^{\infty}{X(f - \text{nf}_{s})}$
$X_{s\omega}(f) = X_{s}(f) \ast F(\Pi(\frac{t}{T}))\begin{matrix} & & \Pi(f) = F \\ \end{matrix}(\Pi(\frac{t}{T}))$
worse than Xs(f) as approximation of X(f).
As an estimation of X(f), does Xsω(f) have picket fence effect? No!
DFT: discrete frequencies (not blocked by the fence).
10-3 Examples Illustrating the computation of the DFT
(Preparation for Mathematical Derivation of FFT)
Properties of WNm:
(2)WNN + m = WNm
Example 10-3: Two-Point DFT
x(0), x(1): $X(k) = \sum_{n = 0}^{1}{x(n)W_{2^{\text{nk}}}}\begin{matrix} & & k = 0,1 \\ \end{matrix}$
x(0), x(1), x(2), x(3)
$\begin{matrix} X(1) = \sum_{n = 0}^{3}{x(n)W_{4^{n}}} = x(0)W_{4^{0}} + x(1)W_{4^{1}} + x(2)W_{4^{2}} + x(3)W_{4^{3}} \\ \text{\ \ \ \ \ \ \ \ } = x(0) - \text{jx}(1) - x(2) + \text{jx}(3) \\ \end{matrix}$
Z(1) = z(0) - z(1) = x(0) - x(2)
v(0) = x(1), v(1) = x(3) => V(0) = v(0) + v(1) = x(1) + x(3)
Four – point DFT Two-point DFT
X(3) = Z(1) + jV(1)
=>$\begin{matrix} \left\{ g(0),g(1),\cdots,g(\frac{N}{2} - 1)\begin{matrix} & & - \text{enen} & \frac{N}{2} & \text{po}\text{int}s \\ \end{matrix} \middle| \right.\ \left\{ ((x(0),x(2),\cdots,x(N - 2))\begin{matrix} & & (g(r) = x(2r)) & & \\ \end{matrix} \middle| \right.\ \left\{ h(0),h(1),\cdots,h(\frac{N}{2} - 1)\begin{matrix} & & & - \text{odd} & \frac{N}{2} & \text{po}\text{int}s \\ \end{matrix} \middle| \right.\ \\ \end{matrix}$
$\begin{matrix} X(k) = \sum_{n = 0}^{N - 1}{x(n)W_{N^{\text{kn}}}} \\ \text{\ \ \ \ \ \ \ \ \ } = \sum_{r = 0}^{\frac{N}{2} - 1}{g(r)W_{N^{k(2r)}}} + \sum_{r = 0}^{\frac{N}{2} - 1}{h(r)W_{N^{k(2r + 1)}}}\begin{matrix} & \\ \end{matrix}(k = 0,1,\text{.}\text{.}\text{.},N - 1) \\ \text{\ \ \ \ \ \ \ \ \ } = \sum_{r = 0}^{\frac{N}{2} - 1}{g(r)W_{N^{2\text{kr}}}} + W_{N^{k}}\sum_{r = 0}^{\frac{N}{2} - 1}{h(r)W_{N^{2\text{kr}}}} \\ \end{matrix}$
How do we obtain G(k), H(k), for k > N/2-1 ?
G(k) = G(N/2+k) k <= N/2-1
Future Decimation
$\begin{matrix} g(0),g(2),\cdots,g(\frac{N}{2} - 2) \\ \text{ge}(0),\text{ge}(1),\text{.}\text{.}\text{.}\text{ge}(\frac{N}{4} - 1) \\ g(1),g(3),\cdots,g(\frac{N}{2} - 1) \\ \text{go}(0),\text{go}(1),\text{.}\text{.}\text{.}\text{go}(\frac{N}{4} - 1) \\ \end{matrix}$ $\begin{matrix} G(k) = \sum_{r = 0}^{\frac{N}{2} - 1}{g(r)W_{{(\frac{N}{2})}^{\text{kr}}}} \\ \sum_{m = 0}^{\frac{N}{4} - 1}{\text{ge}(m)W_{{(\frac{N}{4})}^{\text{km}}}} \\ + W_{{(\frac{N}{2})}^{k}}\sum_{m = 0}^{\frac{N}{4} - 1}{\text{go}(m)W_{{(\frac{N}{4})}^{\text{km}}}} \\ \text{GE}(k) + W_{{(\frac{N}{2})}^{k}}\text{Go}(k) \\ \end{matrix}$
even indexed g odd indexed g
even indexed odd indexed
h (N/4 point) h (N/4 point)
x(0), x(1), … , x(N-1) N = 2m
$\begin{matrix} X(k) = \sum_{n = 0}^{N - 1}{x(n)W_{N^{\text{nk}}}} \\ \text{\ \ \ \ \ \ \ \ \ } = \sum_{n = 0}^{\frac{N}{2} - 1}{x(n)W_{N^{\text{nk}}}} + \sum_{n = \frac{N}{2}}^{N - 1}{x(n)W_{N^{\text{nk}}}} \\ \end{matrix}$
$Y(r) = \sum_{n = 0}^{\frac{N}{2} - 1}{y(n)W_{\frac{N}{2}^{\text{rn}}}}$
X(k) : N-point DFT of x(0), …, x(N) two N/2 point DFT
y(0), y(1), …, y(N/2-1)

(N = 2m) 3Nlog2N real additions
Computation ration
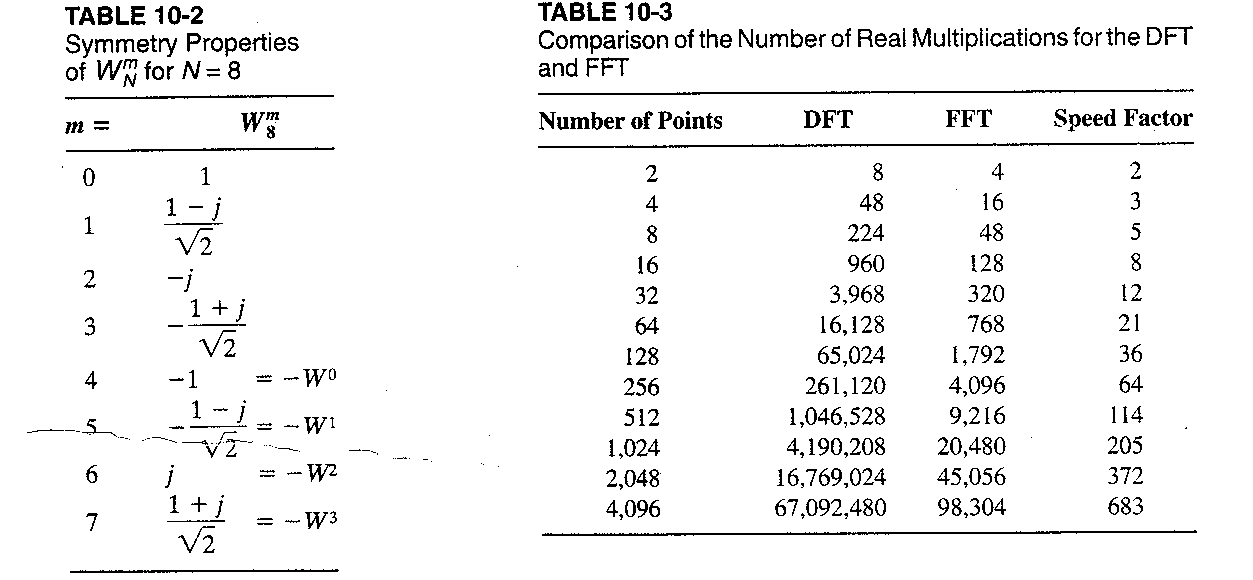
10-5 Properties of the DFT
(3) Subscript e:
Subscript o:
N = 9, xe(n)
$\Rightarrow \frac{N}{2} = 4\text{.}5 \Rightarrow \begin{matrix} \left\{ x(4) = x(5) \middle| \right.\ \left\{ x(3) = x(6) \middle| \right.\ \left\{ x(2) = x(7) \middle| \right.\ \left\{ x(1) = x(8) \middle| \right.\ \\ \end{matrix}$
x(n) - x(N-n) odd ?
Example: N = 9 => N/2 = 4.5
4.5 - (7-4.5) = 9-7 = 2
x(2) + x(7) = x(7) + x(2) ?
subscript i : xi(n) Imaginary part of a complex sequence
left right side:
1. Linearity : Ax(n) + By(n) ↔︎ AX(k) + BX(k)
2. Time Shift: $x(n - m) \leftrightarrow X(k)e^{- j2\pi\frac{\text{km}}{N}} = X(k)W_{N^{k - m}}$
$\text{DFT}(X(n)) = \sum_{n = 0}^{N - 1}{X(n)e^{- j2\pi\frac{\text{nk}}{N}}}$
DFT of x(m)
6. Multiplication
$x(n)y(n)underbracealignl\underset{z(n) = x(n)y(n)}{\overset{\begin{matrix} \begin{matrix} \text{new} & \text{sequence} \\ \end{matrix} \\ \end{matrix}}{\underbrace{}}} \leftrightarrow N^{- 1}\sum_{m = 0}^{N - 1}{X(m)Y(k - m) = N^{- 1}X(k)ΟY(k)}$
(the DFT of an odd real sequence is odd and imaginary )
10. z(n) = x(n) + jy(n)
X(0) = [x(0) + x(2)] + [x(1) + x(3)]
X(1) = [x(0) - x(2)] + (-j)[x(1) - x(3)]
$\begin{matrix} \underset{\Downarrow}{\overset{\begin{matrix} y(0) = 0 & y(1) = 1 & y(2) = 0 & y(3) = - 1 \\ \end{matrix}}{\underbrace{}}} \\ \begin{matrix} Y(0) = 1 & Y(1) = - j2 & Y(2) = 0 & Y(3) = j2 \\ \end{matrix} \\ \end{matrix}$
Example 10-8
Example 10-9: Circular Convolution
$\begin{matrix} x_{1}(n) = 1 & x_{2}(n) = 1 & 0 \leq n \leq N - 1 \\ \end{matrix}$
Filtering
x(0), …, x(N-1) FFT (DFT) =>
$\begin{matrix} x(n) = \sum_{k = 0}^{N - 1}{X(k)e^{j2\pi\frac{\text{nk}}{N}}} \\ \overset{\hat{}(n) = \sum_{k = 0}^{N_{0}}{X(k)e^{j2\pi\frac{\text{nk}}{N}}}}{x} \\ \end{matrix}$
Frequencies with $\omega > \frac{2{\pi N}_{0}}{N}$ have been filtered!
Spectrum Analyzers
Analog oscilloscopes => time-domain display
Parseval’s Theorem
$E = \sum_{k = 0}^{N - 1}\frac{|x(k)|^{2}}{N}$





