Designing and tuning robust feedforward controllers

Take-Home Exam 1: Feedforward for a car cruise

control system under the presence of slope

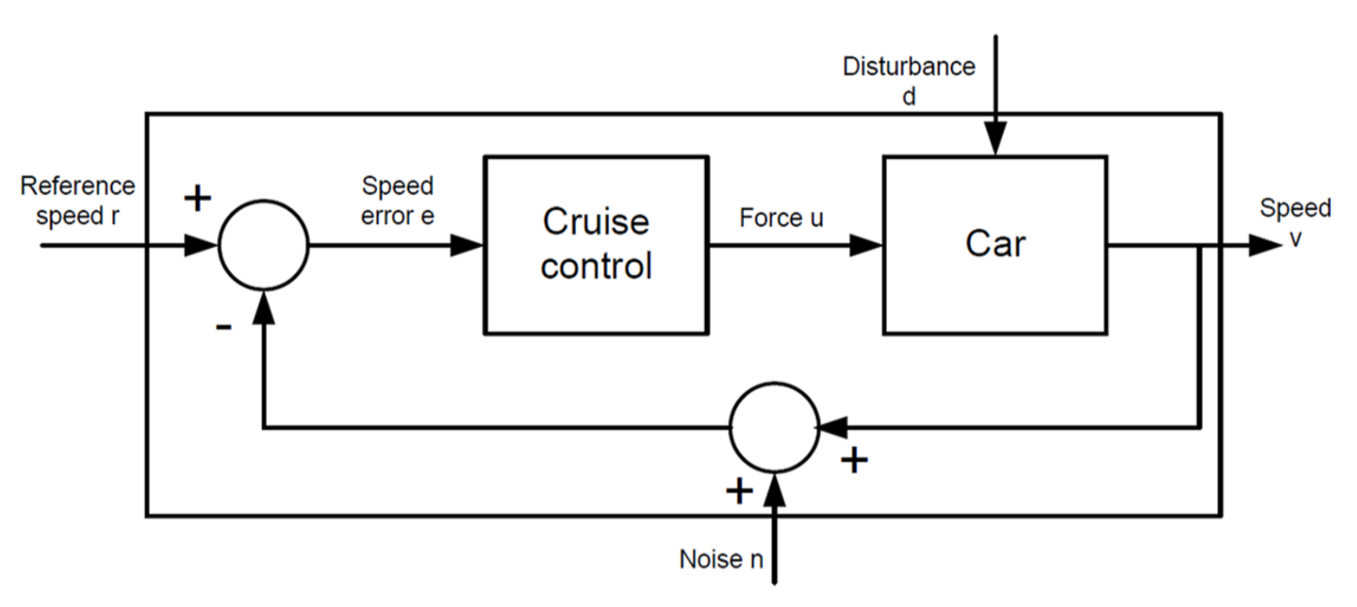
(i) Your group’s report (max. 8 pages)—all given answers should be clearly elaborated together with the reasoning behind them,

(ii) MATLAB and Simulink files that have been used to generate the corre- sponding results shown in your report.

Figure 1: Block diagram for the car cruise control.

However, this car model does not include the presence of disturbances yet. When disturbance is present, it affects the closed-loop dynamics in a way that we do not desire. In this assignment, we will consider a situation where the car model is operating under the influence of slope disturbance.

3 Slope disturbance

The main question for this assignment would be: “Can we come up with a strategy to improve the car cruise control perfor-mance (as shown in Figure 1) under the presence of slope disturbance?”

If we give our cruise control with a certain reference speed, it should maintain such a speed despite the slope disturbances. One way to accomplish this is by utilizing an appropriate disturbance cancellation feedforward controller, under the assumption that the car model Gp(d) is accurate and the slope angle α(t) is measurable.

feedforward controller Cf(s) as:

• Consider a scenario where the slope α(t) varies with the angle about 30 ± 10 degrees. What would be a good Gd(s) to approxi-mate the effect from such slope disturbance? Explain in detail the process you have used to acquire it. Note that such a transfer function Gd(s) will be a linear approximation of a nonlinear mapping. It can be acquired through various means.

– Implement the car model Gp(d) (from Section 2) into the dashed box.

– Run the m-file (‘Closed loop car m.m’), two plots like the ones shown in Figure 5 should appear.

r()=	10	2
r()=	1 + e−3(0.5t−4)	2

y(s) =Gd(s) − Cf(s)Gp(s) 1 + Gp(s)K(s)	d(s)	(3)

α(t) = 30 + 10 sin(t)		(5)

This results in the response shown in Figure 6.

[1] Eduardo Jose Adam and Jacinto L Marchetti. Designing and tuning robust feedforward controllers. Computers & Chemical Engineering, 28(9):1899–1911, 2004.