Cylinder orientation the cylinder vertical and fully submerged

MODULE I:

1. Differentiate Atmospheric Pressure, Gauge Pressure, and Absolute Pressure.

	Definition: Atmospheric pressure is the pressure exerted by the weight of the Earth's atmosphere on a given point. It acts uniformly in all directions. Standard Value: At sea level, it is approximately 101.325 kPa (760 mmHg or 14.696 psi).

	Definition: Gauge pressure is the pressure measured relative to the atmospheric pressure. It indicates the difference between absolute pressure and atmospheric pressure.

	Usage: Commonly used in applications like tire pressure, hydraulic systems, and blood pressure measurements where atmospheric pressure is the reference. Characteristic: Gauge pressure can be positive (above atmospheric pressure) or negative (below atmospheric pressure).

	Formula:

Pabsolute=Pgauge+Patmospheric

Key Differences:


	o
	o	Gauge pressure is relative to atmospheric pressure.
	o	Absolute pressure is relative to a perfect vacuum.

	o
	o

	o	Absolute pressure can theoretically reach zero at a vacuum.
	Applications:
	o
	o
	o

2. Define Fluids, Capillarity, and Surface Tension.

Fluids:

	Characteristics:
	o	Continuity: Fluids continuously deform without a fixed shape.
	o	Compressibility: Gases are highly compressible, whereas liquids are

	o

Capillarity (Capillary Action):


	o	Adhesion: Attraction between fluid molecules and the surface of the

	o	Cohesion: Attraction between fluid molecules themselves.
	Effects: Causes fluids to rise or fall in thin tubes (capillary tubes), allowing phenomena like water transport in plants.

	Definition: Surface tension is the property of a fluid's surface that allows it to resist an external force. It arises due to the cohesive forces between fluid molecules at the surface. Explanation:
	o	Molecules at the surface experience a net inward force because they

	o

	o
	o	Ability of small insects to walk on water.
	o	Minimal surface area configurations, such as spherical shapes in

	Capillarity is influenced by surface tension and adhesive forces. High surface tension can enhance capillary rise. Both phenomena are critical in various natural and industrial processes, including ink flow in pens, absorption of water in soils, and the functioning of biological organisms.

	Pressure Type Measured: Absolute pressure (assuming the open end is at atmospheric pressure).

U-tube Manometer:

Key Differences:


	o	Piezometer: Measures absolute pressure at a single point.
	o	U-tube Manometer: Measures the pressure difference between two
	points.
	o
	o

	o	Piezometer: Provides absolute pressure based on the height of the
	fluid column.
	o	U-tube Manometer: Indicates the pressure difference based on the

	o
	o

4. Explain Total Pressure and Centre of Pressure.

Total Pressure:

	Definition: Total pressure is the sum of the static pressure and the dynamic pressure in a fluid flow. It represents the total energy per unit volume of the fluid. Formula:
	Ptotal=Pstatic+1 2ρv
	o
	o
	o
	Explanation:
	o	Static Pressure: The pressure component acting perpendicular to the

	o

Centre of Pressure:


	o

hc p=I Gˉ
A⋅y
 I G: Second moment of area about the horizontal axis through the centroid

	 

	o

	o	It is generally located below the centroid for submerged surfaces in
	fluids.



	Total Pressure combines both the static and dynamic components, reflecting the overall energy in fluid flow. Centre of Pressure identifies the specific point where the resultant pressure force acts on a surface, essential for understanding force distribution and stability in fluid-structure interactions.

1. Positive Metacentric Height (GM > 0):

o o

o Condition: The metacenter (M) is below the center of gravity (G).

o

Factors Affecting Stability:

	Volume of Displaced Fluid: Changes in submerged volume affect the center of buoyancy (B) and the position of the metacenter (M).

Applications:

	Floating Structures: Designing platforms and buoys to maintain equilibrium in varying sea conditions. Submarines: Controlling buoyancy and center of gravity for stable submergence and surfacing.

	Definition: A streamline is an imaginary line in a fluid flow field that is tangent to the velocity vector of the flow at every point at a given instant.
	o	Instantaneous: Represents the flow direction at a specific moment.

	o
	o	Fixed in Steady Flow: In steady (time-invariant) flow, streamlines
	remain unchanged over time.

 
	o
	through a point over time.
	o	Change with Time in Unsteady Flow: In unsteady flow, streaklines
	can differ from streamlines.

from streamlines and streaklines.

Visualization: Can be tracked by marking a single particle and observing its movement.

	Streakline	Pathline

velocity vectors	particles

instant	through a fixed	particle

	Streamline	Streakline

	Instantaneous	Time-
	Instantaneous
	Smoke lines in	Continuous	Tracking a
		dye injection at

Behavior in	Remains fixed	Coincides with
			streamlines
	with
	streaklines and

	Changes over	Varies
Unsteady Flow		independently
		from	trajectory
	streaklines and
			streamlines
			and streaklines

Understanding these concepts is crucial for analyzing and visualizing different

aspects of fluid flow, especially in complex and unsteady flow conditions.

Assumptions and Given Data:

1. Conical Vessel Dimensions:

o o	Initial Reading (Empty Vessel): 20 cm Manometric Fluid: Assuming the manometer is filled with Mercury (Hg) (a common choice due to its high density), unless specified otherwise.

o The pressure at outlet A is atmospheric pressure.

	o	The manometer shows a reading of 20 cm, which likely represents a
	difference in mercury levels due to initial conditions or calibration. When the Vessel is Completely Filled with Water:
	o

	o

Solution Approach:
1. Determine the Hydrostatic Pressure Due to Water:

o Hydrostatic Pressure (P):

2. Relate Hydrostatic Pressure to Manometer Reading:

o
o	Δ h=
	Δ h=			ρHg×g
	Δ h=	29,430Pa			≈0.22m=22cm
		13,600 kg/m	3×9.81m/s

Total Manometer Reading=20cm+22cm=42cm

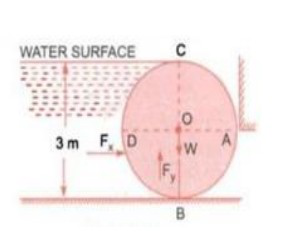
o	Note: The direction of the mercury displacement depends on the configuration of the manometer. If the mercury level on the open side rises, the connected side drops by the calculated Δh, and vice versa.

 The vertical reaction at point B.

Assumptions:
1. Hydrostatic Conditions: The water is at rest, and pressure varies with depth.

o	Point A: Provides a horizontal reaction to balance hydrostatic pressure.

	Point B resists the vertical forces, primarily the weight of the cylinder.

Step 1: Calculate the Hydrostatic Pressure Acting on the Cylinder

 ρ = Density of water

 g = Acceleration due to gravity

2

Where:

 Therefore:

o y1=3 m−1.5 m=1.5m (Top of the cylinder)

F1000 kg/m	2×4m ×		(4.5 2−1.5 2)
H=	2×4m ×		2
FH=1000×9.81×4×		(20.25−2.25)
FH=1000×9.81×4×		2
FH=1000×9.81×4×18 2

FH=353,160N=353.16kN

Interpretation:

Step 2: Determine the Horizontal Reaction at Point A (RA)

 Horizontal Reaction (RA) must balance the hydrostatic force.

 The vertical reaction must balance the weight of the cylinder.

RB=W =196.2kN