Coupling and bending stiffness matrices
Round 2: Composite Materials
Introduction
There are many applications for composite materials ranging from consumer products like sports racquets and bicycle frames to large-scale structures like high-performance car chassis and helicopter fuselage. Composite materials are made out of two components – a matrix and fibre reinforcements. The motivation for the use of these advanced materials is due to their light weight yet high strength at the direction of the fibres. Plies of fibres or laminas impregnated with the resin matrix can be stacked to achieve the required strength at specific directions. When heated to the melting point of the resin and under pressure, the resin melts and followed by a cooling process, the two components are consolidated as one solid composite material known as a laminate.
Analysis
| Stress (GPa) |
|
|
||
|---|---|---|---|---|
| Strain (mm/mm) |
|
Some of the first few stress-strain measurements are shown above. Applying a linear least- squares polynomial, determine the regression equation. Use a table to perform your calculations and plot the data including the regression line with appropriate axis labels and
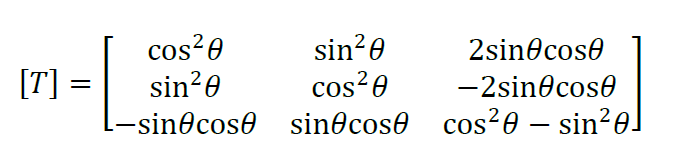
The new or generic stiffness matrix [S] is given as [T]-1[Q][T]. Evaluate [T]-1 and using the material properties of the lamina given above, write a Python function which receives an input θ and returns [S].
Task 5 Four laminas were stacked in the ply orientation [90°/0°/0°/90°] to form a 4-ply epoxy laminate, Figure 3. The thickness of each ply was found to be 0.25 mm.
 x-direction
x-direction
Figure 4
A, B and D are the extensional, coupling and bending stiffness matrices, respectively. N is the in-plane forces per unit length matrix while M is the bending moments per unit length matrix. ε0 is the mid-plane strain matrix while κ is the curvature matrix. Note that N, M, ε0 and κ, each has three components (xx, yy and xy). Write a Python function that finds the combined extensional-bending stiffness matrix C.
D is the diagonal matrix of A while L and U are the strictly lower and upper triangular parts of A, respectively. These three matrices can be obtained using diag, tril, and triu from Numpy. Write a Python function based on this concept and find the mid-plane shear strain ε0xy for the laminate configuration in Figure 3 for 0 ≤ Nxx ≤ 100 N/m starting with initial guesses of 0 for all the required parameters. Consequently, plot ε0xy vs. Nxx with appropriate axis labels and comment on the trend of the shear strains at mid-plane.
Submission
Submit a report detailing your analysis, code and results for Tasks 1 to 8. This report should be brief but well-structured, so that the we can easily interpret your results. Include your Python code as well.





