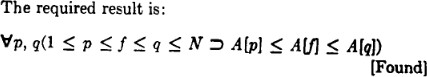Could infer invariant for that location

Invariant Detection

#1

Motivation

#3

Finding Invariants Manually

• Some intermediate invariants:

“Reading Quiz”

• What is “FIND” all about?

• Given a program location, if we could infer an invariant for that location, we could have … – Loop invariants (location = loop head)
– Function pre-conditions (location = entry)
– Function post-conditions (location = exit)
• Can we do this automatically?

– An indicative workload

– High-coverage test cases

• Given:
– while b do c
• Instrument:
– while b do (print Inv1; print Inv2; … ; c)
– Run on all tests, filter out on false
• How many candidate invariants are there?

• At most three variables at a time: finite!
#11

Daikon

#12

Daikon Weaknesses• What could go wrong?

• Nothing prevents Daikon from finding these• But each increase in the language of
candidate invariants bloats the runtime

• False Positives from linguistic coincidence– Ex: ptr % 4 == 0
– Ex: x <= MAX_INT
– Not false, but not related to correctness.

#15

induce invariants via constraint solving

– Ex: instead of printing x>y, x<y, x>=y, etc., just print out x and y and figure out which is true later

Dig

Dig Example: Cohen's Division // quotient

// remainder

// loop invariant