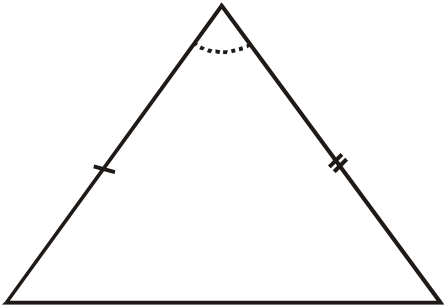
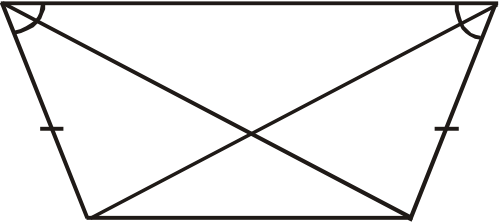
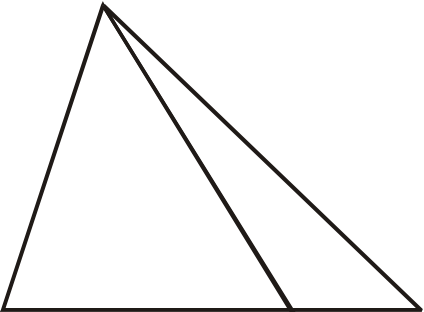
Cfand aeb afc oto prove abc isosceles abe and acf
|
Class IX_Mathematics |
|---|
Triangle
A
B C
C
“CPCT” means corresponding parts of congruent triangles.
B C E F If in ∆sABC and DEF, AB = DE, AC = DF and ∠BAC = ∠EDF
Then, ABC≅ ∆DEF . It is called SAS congruence rule i.e. side-angle-side]To Prove:ABC≅ ∆DEF Fig.1
Proof:Case – (i)
Let AB = DE [Assumed]
|
C | D |
|
|---|---|---|---|
| A | |||
| P | |||
| B | |||
| Mathematics, Class : IX |
|---|
But it is given that ∠ACB = ∠DFE
∴∠ACB = ∠PCB which is not possible.i.e. it is only possible if P coincides with A
⇒ BA = ED
Hence, ABC≅ ∆DEF [by SAS rule]
Case – (iii)
If AB < DE, we can choose a point M on DE such that ME = AB and repeating the arguments as given in case (ii), we can conclude that AB = DE and, hence, ABC≅ ∆DEF Now, two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal. We may call it as Angle-Angle-Side (AAS).
| B | F | E |
|---|
In ∆ABC altitudes BE = CF
To prove: (i) ABE≅ ∆ACF
(ii) AB = AC ; i.e. ABC is an isosceles triangle.Solution:
(i) In ∆ABE and ∆ ACF, we have
BE = CF [Given]
∠AEB = ∠AFC = 90o [ BE and CF are altitudes: Given] and ∠A = ∠A [Common]
| 3 3 |
|---|
C E
| B | 3 |
|
|
|---|---|---|---|
|
|||
| 4 4 |
|---|
A D
B
C E
F If ABC and DEF are two right triangles in which
∠B = ∠E = 90o, AC = DF and AB = DE
| ≅ ∆DEF |
|---|
A
B
Given:
ABC is a right angled triangle in which ∠A = 90o and AB = AC.To find: ∠B and ∠C
Solution:
In right angled triangle ABC, we have
AB = AC [Given]
∴∠B = ∠C
[Angles opposite to equal sides of a triangle are equal] ....(i) Now, ∠A + ∠B + ∠C = 180o [Angles sum property of a ∆] ⇒ 90o + ∠B + ∠B = 180o [From (i)
∠B = ∠C]
⇒ 2∠B = 180o – 90o⇒ 2∠B = 90o
Hence, ∠B = ∠C = 45o
|
5 5 |
|---|
Construction: AD bisector of ∠A is drawn at BC i.e. ∠BAD = ∠CAD Proof: In ∆BAD and ∆CAD, we have
AB = AC [Given]
∠BAD = ∠CAD [By construction]
and AD = AD [Common]
| ∴ ∆BAD | ≅ ∆CAD |
|
|---|
B C Let ABC be a triangle in which AC > AB and AC > BC.
| Mathematics, Class : IX |
|---|
The side opposite to the largest angle is the longest.
LEARN IT
Theorem: The sum of any two sides of a triangle is greater than the third side.
Solution:
For ∆ABC and ∆ADC, we have AB = AD
∠BAC = ∠DAC
AC = AC
Therefore, by SAS criteria, we have ∆ABC ≅∆ADC
Also, we have corresponding parts of the two triangle equal and it gives BC = DC.
| Illustration-5: | B |
|
A | |
|---|---|---|---|---|
| C |
| 7 7 |
|---|
| m | A | B | l | ||
|---|---|---|---|---|---|
|
|||||
| n | C | n | |||
| l | |||||
| m |
Solution:
Let us consider ∆PAB and ∆PAC (as shown in figure 7.35) Here, we have PB = PC (Given)
∠PBA = ∠PCA (Each = 90º)
PA = PA (Common side)
Then by RHS congruence criteria, We have
∆PAB ≅∆PAC.
| ∠C | > | 1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | |||||||||||
| | ∠PCB | = | 1 | ∠C and PBC | = | 1 |
|
||||
|
2 | 2 | |||||||||
| as PB and PC are bisectors of B and C | |||||||||||
|
Mathematics, Class : IX | |
|---|---|---|
| Illustration-8: | B | A |
An exterior angle of a triangle is Now, ∠ADC > ∠ABD ... (2) greater than an opposite interior angle From (1) and (2)
∠ACD > ∠ABD
i.e., ∠ACD > ∠ABC
i.e., in ∆ABC,
∠C > ∠B
⇒ AB > AC
⇒ AB > AD ….(1)
Similarly, in right angled ∆ABC and ∆CFA, we have BC > BE ….(2)
….(3) and CA > CF
Adding (1), (2), (3)
AB + BC + CA > AD + BE + CF
i.e., Perimeter of ∆ABC > (AD + BE + CF).Illustration-10:
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
|
Mathematics, Class : IX |
|---|---|
|
Solution:
AD is an altitude from vertex A on BC
∴∠ADB = ∠ADC = 90o
(i) Now, in right ∆sADB and ADC ,
we have
∠ADB = ∠ADC = 90o [Given]
and AD = AD [Common]
∴ ∆ADB≅ ∆ADC[By RHS congruence rule]
∴ BD = CD [By CPCT]
Hence, AD bisects BC. Proved.
| Illustration-11: | B | A | E | C | |
|---|---|---|---|---|---|
|
|||||
|
|||||
| Mathematics, Class : IX | ||
|---|---|---|
|
||
|
Mathematics, Class : IX |
|---|
KEY POINTS
| 12 12 |
|---|
4. The sum and difference of two angles of a triangle are 128° and 22° respectively. Find all the angles of the triangle.
|
|
|
|---|---|---|
|
||
| B | C | |
|
||
|
||
| 13 13 |
|---|
| *3. | B | C | |||
|---|---|---|---|---|---|
|
|||||
|
D | E |
|||
|
|
||||
| D | |||||
| A | D | ||||
|
B | F |
|
||
| C | B | ||
|---|---|---|---|
| A | P | ||
|
|||
| Y respectively and ∠ABX = ∠PQY. Prove that | |||
|
|||
| (i) | (ii) | ||
| 15 15 |
|---|
| 16 16 |
|---|
A
| *9. |
|
S | A | R | P | |
|---|---|---|---|---|---|---|
| 10. | ||||||
|
17 17 |
|---|
1. 2. |
|||
|---|---|---|---|
| (A) 60º | (B) 45º | ||
| (C) 30º | (D) 90º. | ||
|
|||
(D) 1/2(∠R).
| (B) 70º | ||
|---|---|---|
|
(D) 80. | |
| Mathematics, Class : IX | ||
|---|---|---|
| 6. |
|
|
| 8. |
|
A |  |
|
|---|---|---|---|---|
| B | ||||
9. The triangle formed by joining the mid-points of the sides of an isosceles triangles is
(A) scalene triangle (C) right triangle
| 19 19 |
|---|
15. 16. |
In ∆ABC, ∠B = 45º, ∠C = 55º and bisector of ∠A meets BC at a point D. Find ∠ADC. | |||||
|---|---|---|---|---|---|---|
|
||||||
|
||||||
2 |
− | . Then which is not the value | ||||
|
|
|||||
|
A |
|
||||
| H | K | |||||
| B | C | |||||
MATRIX & MATCHING
| 20 20 |
|---|