Your Question:

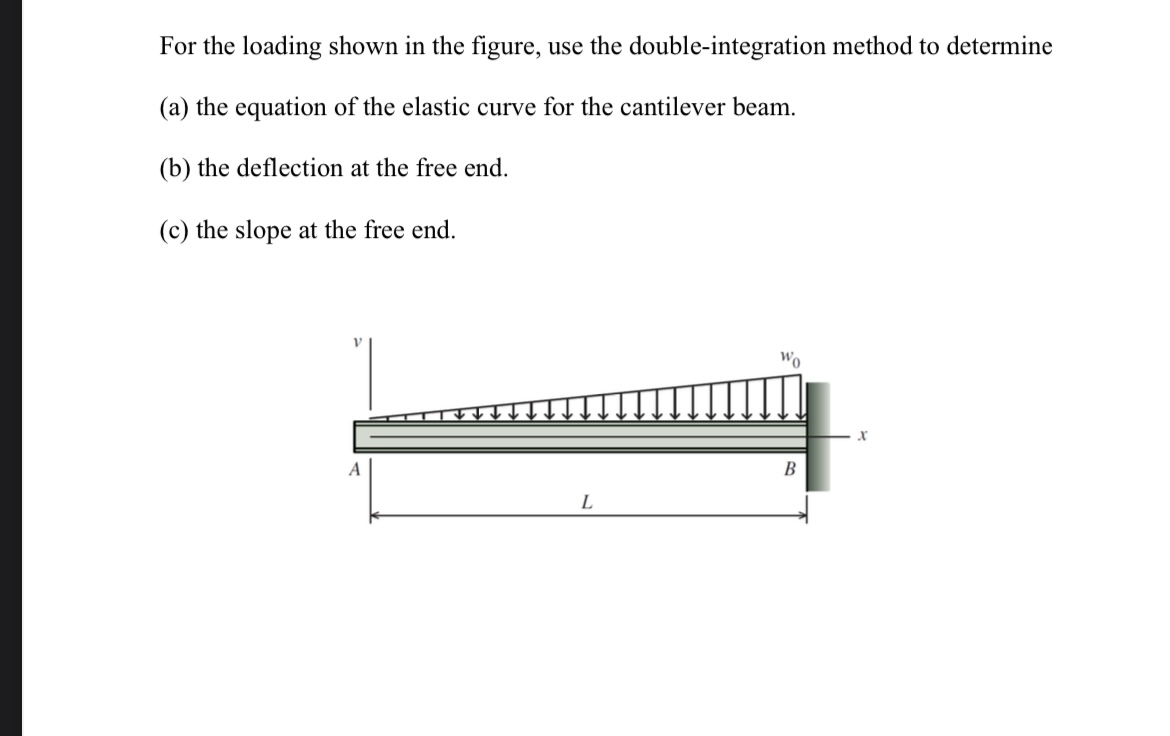
For the loading shown in the figure, use the double-integration method to determine.

(a) the equation of the elastic curve for the cantilever beam.

Step By Step Answers with Explanation

To determine the slope at the free end of the cantilever beam shown in the figure using the double integration method, we will first need to determine the equation of the elastic curve for the beam.

Step 1: Determine the bending moment equation

• L is the length of the beam

• x is the distance from the free end of the beam

M = -10x

Step 2: Determine the slope equation

• I is the moment of inertia of the beam cross-section

• y is the deflection of the beam at a distance x from the free end

where C1 is a constant of integration.

Step 3: Determine the deflection equation

To determine the values of the constants of integration C1 and C2, we need to apply the boundary conditions for the beam. The boundary conditions for a cantilever beam with a point load at the free end are:

y(0) = 0

C2 = 0

Applying the second boundary condition, we get:

y = -5x^3/3

Step 5: Determine the slope at the free end

Therefore, the slope at the free end of the cantilever beam shown in the figure is -20 kN-m/rad.

450-word explanation

∫_a^b f(x) dx = F(b) - F(a)

The double integration method for solving differential equations works by integrating the differential equation twice. The first integration gives us the slope equation, and the second integration gives us the deflection equation.

To solve the equation of elastic equilibrium using the double integration method, we first need to integrate it once. This gives us the slope equation:

EI dy/dx = M

Once we have the deflection equation, we can apply the boundary conditions for the beam to determine the values of the constants of integration. The boundary conditions are typically specified at the supports of the beam.

Once we have determined the values of the constants of integration, we can use the deflection equation to calculate the deflection of the beam at any point along its length. We can also use the slope equation to calculate the slope of the beam at any point along its length.

cantilever beam with a point load at the free end

The bending moment equation for this beam is given by:

x is the distance from the free end of the beam

Substituting the bending moment equation into the slope equation, we get:

Applying the boundary condition y(0) = 0, we get:

C1 = 0

Therefore, the slope at the free end of the beam is -20 kN-m/rad.

Conclusion