Calculate the equivalent single-phase frictional head loss

 If you underestimate frictional
losses along a pipeline, you

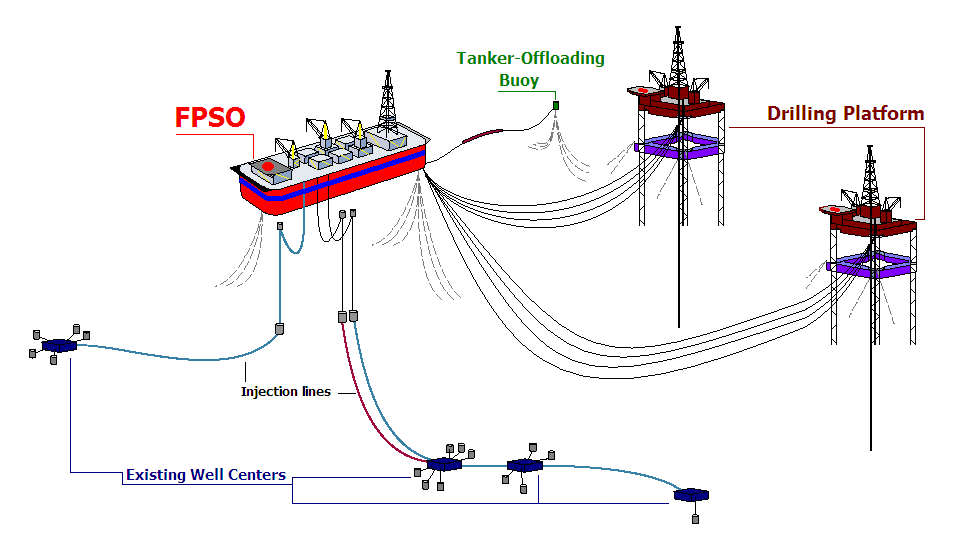
[Gunnernett http://en.wikipedia.org/wiki/File:FPSO_diagram.PNG] losses in a pipeline, you

 could have made the pipe D
smaller or the lines longer;

empirical models.

	Experimental conditions vs. field conditions.

 3 categories/approaches for modelling 2-phase flow Category 1: pseudo-single phase flow models (no slip) Category 2: separated flow models (allow slip)
 Category 3: consider both flow patterns and slip

 Hagedorn & Brown (1964) correlation

 Beggs & Brill (1973) correlation

	EG55F8/G8 Flow Assurance 2020/21

 The phases are modelled as a single, pseudo-fluid.

 Assume that pseudo-fluid flow can be described by conventional equations for single-phase flows by defining appropriate effective properties.

 Elevation head loss/gain
 Use the no-slip mixture density

 Frictional head loss

ρ	u		d	u		=	G	d		G		=	G	2	d		1		=		m	g	+	m l		2	d		1	
h		h			h					ρ h							ρ h						A						ρ h	 


	EG55F8/G8 Flow Assurance 2020/21

	EG55F8/G8 Flow Assurance 2020/21

DA: I will go through this worked example, and the derivation of the two-phase multiplier for homogenous flow (the next slide) in the online workshop on 3/3/2021
(or see Blackboard Collaborate Ultra on MyAberdeen for the recording)



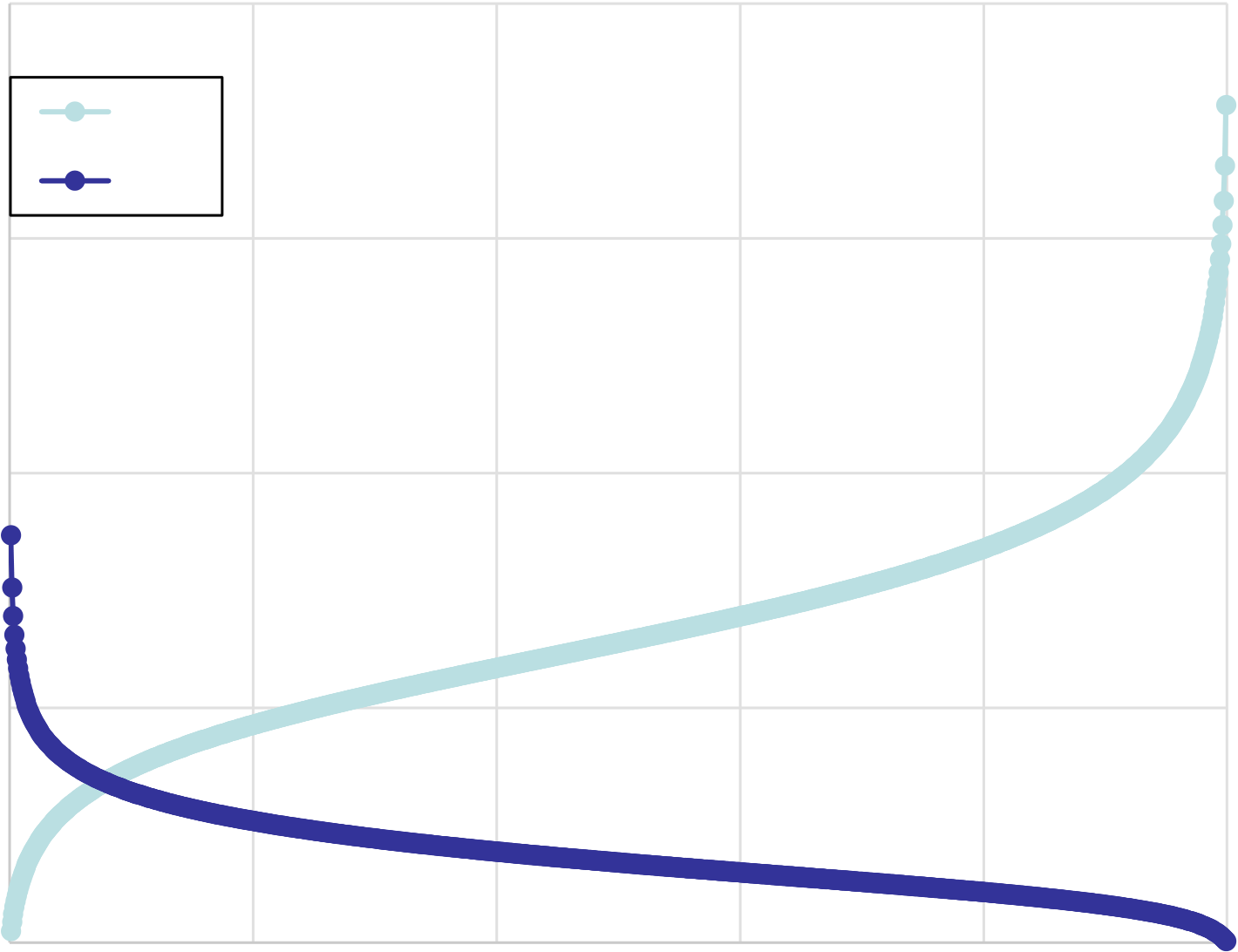
two-phase multiplier:

 Two-phase multipliers as a function of mass quality

−		d p	h	= −	d p		Φ	2		10000
		d s			d s			l	er φ2	1000	Phi_l
								l			phi_g
							l
−		d p	h	= −	d p		Φ	2
		d s			d s		Φ	g	Two-phase multiplier φ2	100			0.4	0.6	0.8	1
		d s					g			100
										10
 total mass flux										10
 pipe diameter										1


 liquid viscosity												mass quality x
												mass quality x

 3 categories/approaches for modelling 2-phase flow Category 1: pseudo-single phase flow models (no slip) Category 2: separated flow models (allow slip)
 Category 3: consider both flow patterns and slip

	EG55F8/G8 Flow Assurance 2020/21

gu



ρ tptp u

ρ tp



pipes.

	Lockhart & Martinelli (1949): steady, incompressible, horizontal gas/liquid flow.




		EG55F8/G8 Flow Assurance 2020/21

−ρ tp		Φ	2	ρ l g		−	d h f,l				=		Φ		2	ρ g		g			d h f,g			  
−ρ tp	d s	Φ	L	ρ l g		−	d s				=		Φ		G	ρ g		g			d s			  
=		Φ	2			2C		f,l	u sl 2			=	Φ	2		ρ g	g			2C		f,g	u sg 2		  
=		Φ	L			gD							Φ	G		ρ g	g			gD					  



 What multiplier should we use?

	EG55F8/G8 Flow Assurance 2020/21

Lockhart and Martinelli (1949):
 correlated pressure drop data from
pipes 25 mm (1 in) in diameter or
less within about 650 percent.

	In general, the predictions are high


pipe diameters up to about 0.1 m (4

in) with about the same accuracy.	Martinelli parameter

 What multiplier should we use?

 Calculate the Lockhart-Martinelli parameter X

Φ = + L			C		1						20 12
			C		1						20 12
			X		X		2	2		where C	= 
Φ	2	= +	X		X		2
	2		CX	+		X
	G		CX	+		X

 Procedure:
1. Calculate Rek for each phase.

2. Calculate the equivalent single-phase frictional head loss.

v sg		=	Q g	=	4 0.835	=
v sg		=	A	=	π D
v sl	=		Q l	=	4 0.0368	=	0.323 m/s
v sl	=		A	=	π D