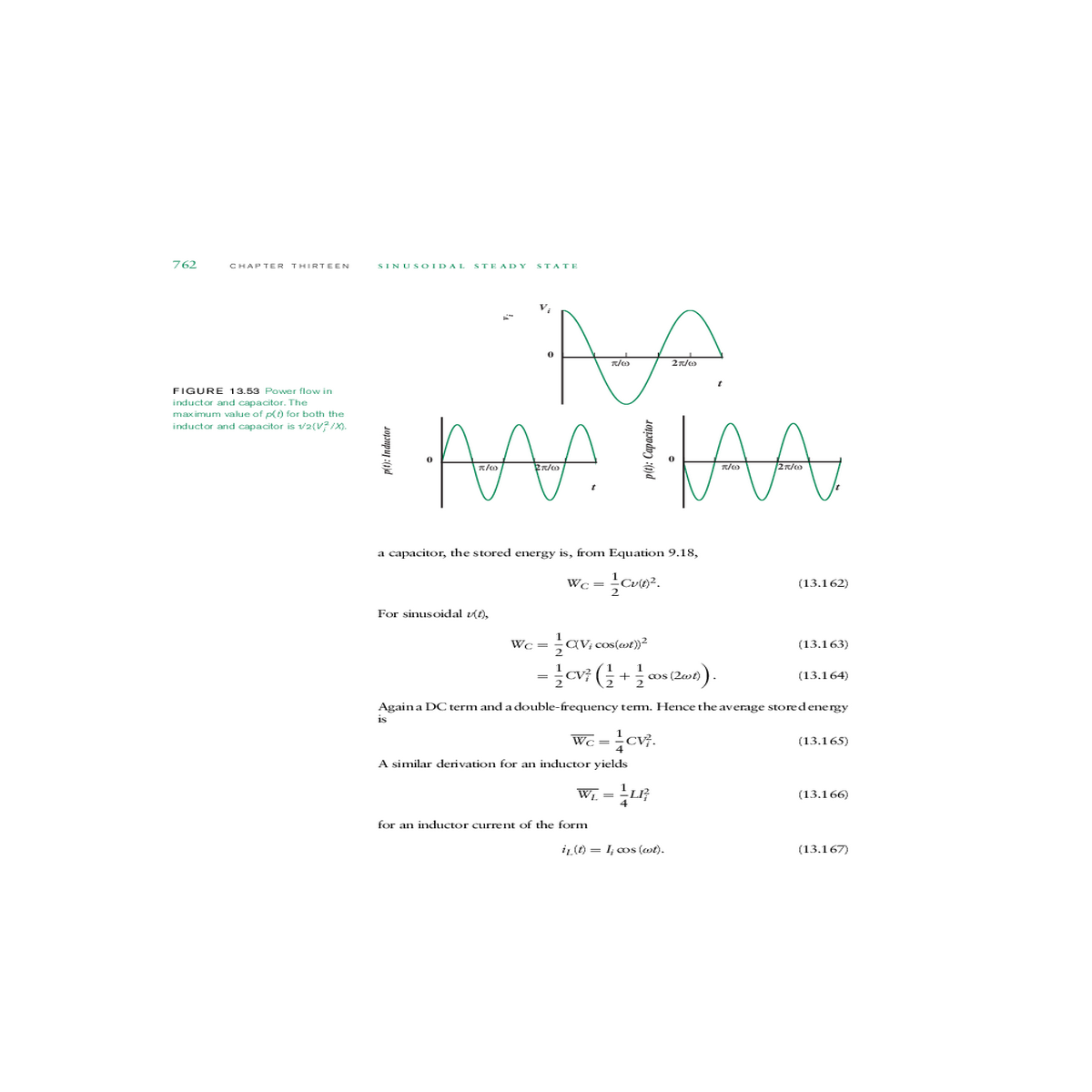
And equation with becomesthe power waveform depicted figure

762	C H A P T E R	s t e a d y
762	C H A P T E R	vi	Vi
FIGURE 13.53 Power flow in			Vi
FIGURE 13.53 Power flow in			0

inductor and capacitor. The

maximum value of p(t) for both the	p(t): Inductor	0	π/ω	2π/ω	t	p(t): Capacitor		π/ω	2π/ω	t
inductor and capacitor is 1/2(V2 i/X).	p(t): Inductor	0	π/ω	2π/ω	t	p(t): Capacitor		π/ω	2π/ω	t

WC =1		(13.162)

WC =1	C(Vi cos(ωt))2			(13.163)
	C(Vi cos(ωt))2			(13.164)
	CV2 i	�1	+1
=1	CV2 i	�1	+1

Again a DC term and a double-frequency term. Hence the average stored energy is

WC =1		(13.165)

WL =1		(13.166)

iL(t) = Ii cos (ωt). (13.167)

				13.7 Power and Energy in an Impedance			763
					p		763
						FIGURE 13.54 Power flow in an
						inductive circuit. The average
						1/2V2 the minimum value is
0	π/ω	2π/ω	t
				π/ω
				t

For the general case when the network contains resistors, capacitors, and induc-tors, the power flow will have some intermediate form between Figure 13.52 and Figure 13.53. Assuming that the circuit is net inductive at the frequency of

interest, then θ is positive but less than π/2, and Equation 13.149 with φ = 0 becomes
13.7.4

			i(t)			C
Ii =Vi = R + 1/jωC (13.168) θ = tan−1�ωRC� (13.170) 1			i(t)			C
				+	R
				-	R
			I		1/jωC		R
			Vi				R
			Vi
p1	V2 i cos(θ)	(13.171)	FIGURE 13.55 Series RC
=	�V2 i R2+ (1/ωC)2 cos(θ)
=1	�V2 i R2+ (1/ωC)2 cos(θ)	(13.172)