Your Question:

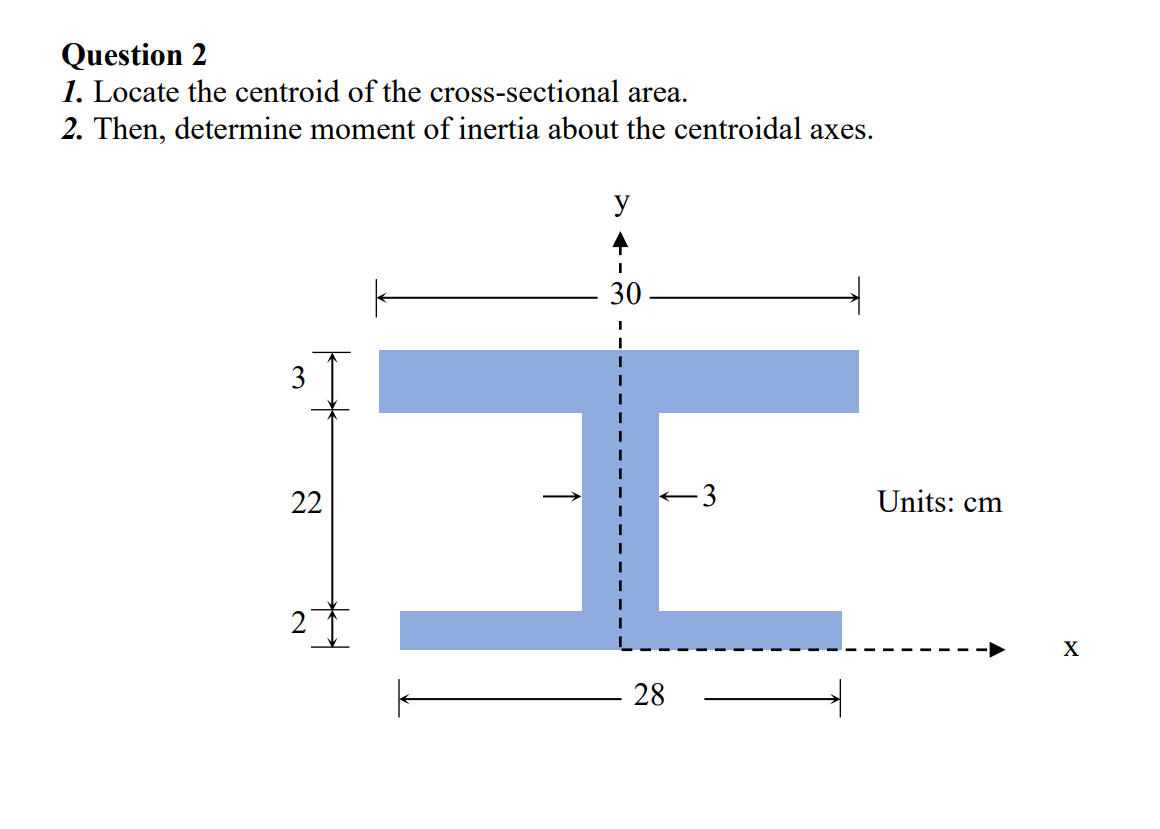
Question 2

1. Locate the centroid of the cross-sectional area.

3

22 22

Step By Step Answers with Explanation

1. Locate the centroid of the cross-sectional area.

To locate the centroid of the cross-sectional area, we can use the following steps:

1. Divide the cross-sectional area into simpler shapes, such as rectangles and triangles.

Step 2: Calculate the centroid of each simpler shape.

The centroids of the rectangles and the triangle are shown below:

Centroid = (180, 90) / 80

Centroid = (2.25, 1.125) cm

2. Determine moment of inertia about the centroidal axes.

3. Sum the moments of inertia of the elemental areas.

Step 1: Divide the cross-sectional area into elemental areas.

Step 3: Sum the moments of inertia of the elemental areas.

The moment of inertia of the cross-sectional area about the centroidal axes is calculated as follows:

Calculation of moment of inertia about the centroidal y-axis:

Moment of inertia about y-axis = 1/12 * (30 * 22^2 + 22 * 30^2 + 28 * 3^2)