Computer Science 220S2C Python Programming

{`
Computer Science 220S2C (2018) 
Assignment 3 (Graph Algorithms) 
`}

Automarker Submission

This assignment tests your understanding of graph optimization problems. To get marks for this assignment you need to submit three programs for the following tasks to http://www.cs.auckland.ac.nz/automated-marker twice. Note this marker runs on a linux box so no Microsoft speciﬁc code should be used; read the help/FAQ for more details. Each program will have an easy test case (2 marks) and harder test case (1 mark). Please use the suﬃx E of your program basename to denote ‘E’asy (test data) and H to denote ‘H’ arder (test data). For Task 1, name your source code mstE.ext and mstH.ext, where ext denotes one of {java, cpp, py, cs} to indicate a java/c++/python/c#(mono) program. For Task 2, name your source code named maxpathE.ext and maxpathH.ext, respectively. For Task 3, please submit source code named snakeE.ext and snakeH.ext, respectively. An excessive number of submissions (over 10) for a particular problem will accrue a 20% penalty per that problem if you eventually solve it.

Task 1: Minimum Spanning Trees

For this warm-up task you are to implement any eﬃcient minimum spanning tree algorithm that takes a sequence of edge-weighted graphs and outputs the minimum cost weight of a spanning tree of each.

Input Format

For this assignment we use adjacency matrices with positive integer weights. Here a zero entry at row i and column j indicates that no edge ij exists in the graph. The ﬁrst line consists of an integer n ≤ 1000 denoting the order of the graph. This is then followed by n lines of n white-space separated integers denoting edge weights. The sequence of graphs is terminated by a value n = 0, which is not processed.

{`
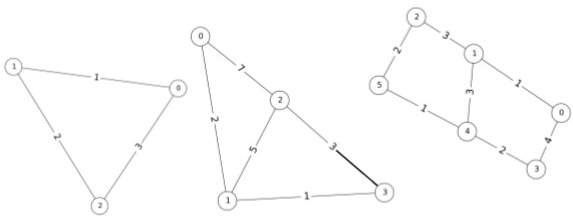
3
0 1 3 
1 0 2
3 2 0
4
0 2 7 0
2 0 5 1
7 5 0 3
0 1 3 0
6
0 1 0 4 0 0
1 0 3 0 3 0
0 3 0 0 0 2 
4 0 0 0 2 0
0 3 0 2 0 1
0 0 2 0 1 0
0
`}

Output Format

Output should be one line for each input graph indicating the minimum cost weighted tree. The sample output for the previous input cases is as follows.

3
6
9

Task 2: A Paths Optimization Problem for Weighted Trees

A developer has designed a subdivision within a city such that all roads connect at intersections in a treelike design. This is to prevent all petrol-head hooligans from disturbing the residences by not having any road loops for races. Only the entering intersection is connected to the rest of the city. The developer is selling oﬀ land alongside roads between adjacent intersections. A real estate agent has produced a green book indicating the expected dollar proﬁt (positive, zero or negative) that can be obtained by purchasing the land alongside each road. Potential buyers want to maximize their proﬁt, but prefer to buy a contiguous stretch of land alongside a simple road chain that connects two intersections of the subdivision. Your task is to write a program to determine the maximum non-negative proﬁt that can be obtained this way. As an example, consider the following representation of a subdivision, where road labels represent expected proﬁts. In this scenario, the maximum non-negative proﬁt is 5, and can be obtained alongside the emphasized roads:

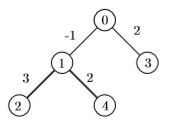
Input Format

Input for this problem consists of a sequence of one or more scenarios, taken from the keyboard/stdin. Each scenario contains two or more lines. • The ﬁrst line contains an integer n, 1 ≤ n ≤ 500000, indicating the number of intersections, including the entrance intersection, implicitly labelled 0. • This is then followed by one or more lines, containing n−1 pairs of integers. All integers are separated by single spaces or newlines. The y-th intersection is deﬁned by the y-th pair of integers ‘x p’, where 1 ≤ y < n, 0 ≤ x < y, −1000 ≤ p ≤ 1000. This pair indicates that a road is added between y and a previously deﬁned intersection, x, with a green book proﬁt value given by p.

The input will be terminated by a line consisting of one zero (0). This line should not be processed. Some sample input scenarios follows.

{`
5 
0 -1 1 3 0 2 1 2 
5 
0 1 1 -3 0 -2 1 -2 
5
0 -1 1 -3 0 -2 1 -2 
10 
0 -1 0 -1 0 0 1 3 1 4 2 4 2 2 3 
3 3 3 
0
`}

Output Format

Output will be a sequence of lines, one for each input scenario. Each line will contain an integer, indicating the maximum non-negative proﬁt sum, over all possible simple road chains connecting two intersections of the subdivision. Write zero (0) if no proﬁt can be obtained. The output for the previous sample input follows.

5
1
0
7

Task 3: Snakes in a Graph

For a graph G = (V,E), a snake (also called an induced path) is a path v1,v2,...,vk such that for all j−i > 1 (vi,vj) 6∈ E. That is, it is a sequence of vertices in G such that each two adjacent vertices in the sequence are connected by an edge in G, and each two nonadjacent vertices in the sequence are not connected by any edge in G.

For this task, our goal is to determine the largest snake of a graph.

Input Format

Input for this problem consist of a sequence of one or more (undirected) graphs taken from the keyboard. Each graph is represented by an adjacency list. The ﬁrst line is an integer n indicating the order of the graph. This is followed by n white space separated lists of adjacencies for nodes labeled 0 to n − 1. The input will be terminated by a line consisting of one zero (0). This line should not be processed. Two sample input graphs are listed below. The easy (harder) test cases are graphs of order at most 10 (50).

Output Format

Output will be just one integer per line sent to the console (e.g. System.out). For the above, input we would output the following two integers denoting the longest snake of the two graphs. Recall that the length of a path is the number of edges.

2
3