CCNA Exercise Lab 5
Written Lab
1. Create a static route to network 172.16.10.0/24 with a next hop gate- way of 172.16.20.1 and an administrative distance of 150.
Ans - # ip route 172.16.10.5 255.255.255.0 172.16.20.1 150
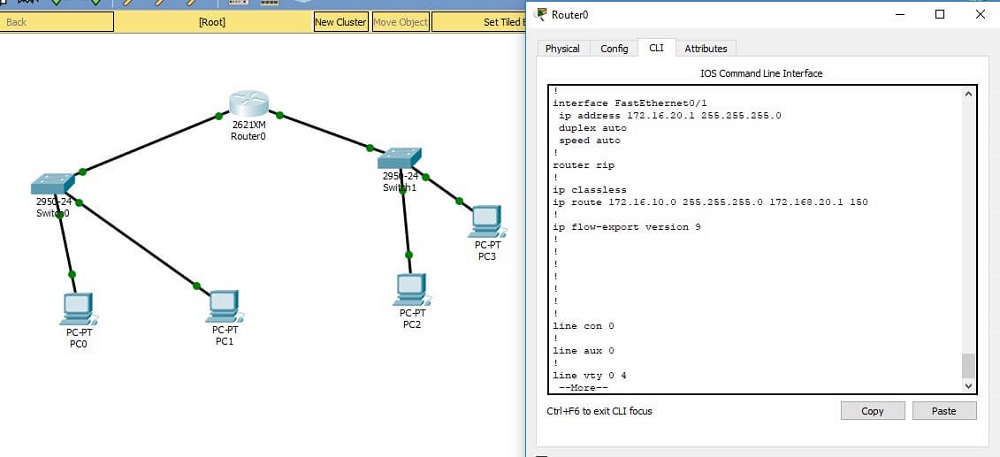
2. Write the commands used to turn RIP routing on in a router and advertise network 10.0.0.0.
Ans – #conf t
#router rip
#network 10.0.0.0
#end
3. Write the commands to stop a router from propagating RIP informa- tion out serial 1.
Ans - #conf t
#router rip
#passive interface fa0/1
4. Write the commands to create an AS 10 with IGRP in your 172.16.0.0 network.
Ans – #conf t
#router igrp 10
#network 172.16.0.0
5. Write the commands to configure a default route on a router to go to 172.16.50.3.
Ans - #conf t
#ip default-network 172.16.50.3
6. What works with triggered updates to help stop routing loops in dis- tance-vector networks?
Ans – Split horizon- it stops the route from being advertise in the direction it is come from to avoid routing loops.
7. What stops routing loops in distance-vector networks by sending out a maximum hop count as soon as a link fails?
Ans- TTL field in IP datagram header
8. What stops routing loops in distance-vector networks by not resending information learned on an interface out that same interface?
Ans – Split horizon
9. The command controls the load balancing between the best metric and the worst acceptable
Ans – variance -command
10. What command is used to send routing updates as they are sent and received on the router to the console session?
Ans - at the configuration mode #passive-interface fa0/0
(Fa0/0 is the interface where you want to send the updates)
Hands-on Labs
In the following hands-on labs, you will configure a network with three 2501 routers and one 2621 router.
The following labs will be covered: Lab 5.1: Creating Static Routes
Lab 5.2: Dynamic Routing with RIP Lab 5.3: Dynamic Routing with IGRP
Figure 5.9 will be used to configure all routers.
FIGURE 5.9 Hands-on lab internetwork
172.16.30.0
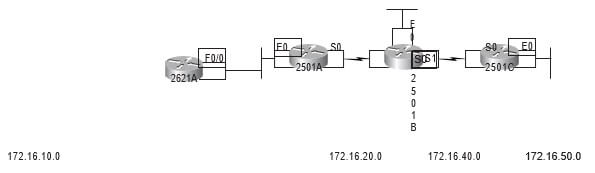
Lab 5.1: Creating Static Routes
In this first lab, you will create a static route in all four routers so that the routers see all networks. Verify with the Ping program when complete.
1. The 2621 router is connected to network 172.16.10.0/24. It does not know about networks 172.16.20.0/24, 172.16.30.0/24, 172.16.40.0/24, and 172.16.50.0/24. Create static routes so that the 2621 router can see all networks, as shown here.
2621#config t
2621(config)#ip route 172.16.20.0 255.255.255.0 172.16.10.1
2621(config)#ip route 172.16.30.0 255.255.255.0 172.16.10.1
2621(config)#ip route 172.16.40.0 255.255.255.0 172.16.10.1
2621(config)#ip route 172.16.50.0 255.255.255.0 172.16.10.1
2. Save the current configuration for the 2621 router by going to the enabled mode, typing copy run start, and pressing Enter.
3. On Router A, create a static route to see networks 172.16.10.0/24, 172.16.30.0/24, 172.16.40.0/24, and 172.16.50.0/24, as shown here.
RouterA#config t
RouterA(config)#ip 172.16.20.2 route 172.16.30.0 255.255.255.0
RouterA(config)#ip 172.16.20.2 route 172.16.40.0 255.255.255.0
RouterA(config)#ip 172.16.20.2 route 172.16.50.0 255.255.255.0
These commands told Router A to get to network 172.16.30.0/24 and use either IP address 172.16.20.2, which is the closet neighbor inter- face connected to network 172.16.30.0/24, or Router B. This is the same interface you will use to get to networks 172.16.40.0/24 and 172.16.50.0/24.
Save the current configuration for Router A by going to the enabled mode, typing copy run start, and pressing
On Router B, create a static route to see networks 16.10.0/24 and 172.16.50.0/24, which are not directly connected. Create static routes so that Router B can see all networks, as shown here.
RouterB#config t
RouterB(config)#ip route 172.16.10.0 255.255.255.0 172.16.20.1
RouterB(config)#ip route 172.16.50.0 255.255.255.0 172.16.40.2
The first command told Router B that to get to network 172.16.10.0/24, it needs to use 172.16.20.1. The next command told Router B to get to network 172.16.50.0/24 through 172.16.40.2. Save the current configuration for Router B by going to the enable mode, typing copy run start, and pressing Enter.
6. Router C is connected to networks 172.16.50.0/24 and 172.16.40.0/24. It does not know about networks 172.16.30.0/24, 172.16.20.0/ 24, and 172.16.10.0/24. Create static routes so that Router C can see all networks, as shown here.
RouterC#config t
RouterC(config)#ip 172.16.40.1 route 172.16.30.0 255.255.255.0
RouterC(config)#ip 172.16.40.1 route 172.16.20.0 255.255.255.0
RouterA(config)#ip 172.16.40.1 route 172.16.10.0 255.255.255.0
Save the current configuration for Router C by going to the enable mode, typing copy run start, and pressing Enter.
Now ping from each router to your hosts and from each router to each router. If it is set up correctly, it will work.
Lab 5.2: Dynamic Routing with RIP
In this lab, we will use the dynamic routing protocol RIP instead of static and default routing.
1. Remove any static routes or default routes configured on your routers by using the no ip route command. For example:
RouterA#config t
|
RouterA(config)#no ip route 255.255.255.0 172.16.11.2 |
172.16.10.0 |
|
RouterA(config)#no ip route 255.255.255.0 172.16.20.2 |
172.16.30.0 |
|
RouterA(config)#no ip route 255.255.255.0 172.16.20.2 |
172.16.40.0 |
|
RouterA(config)#no ip route 255.255.255.0 172.16.20.2 |
172.16.50.0 |
|
RouterA(config)#no ip route 255.255.255.0 172.16.20.2 |
172.16.55.0 |
2. After your static and default routers are clear, go into configuration mode on Router A by typing config t.
3. Tell your router to use RIP routing by typing router rip and pressing Enter, as shown here: config t router rip
4. Add the network number you want to advertise by typing network 172.16.0.0 and pressing Enter.
5. Press Ctrl+Z to get out of configuration mode.
6. Go to Routers B and C and the 2621 router and type the same com- mands, as shown here:
Config t Router rip
Network 172.16.0.0
7. Verify that RIP is running at each router by typing the following com- mands at each router:
show ip protocol show ip route
show running-config or show run
8. Save your configurations by typing copy run start or copy running- config startup-config and pressing Enter at each router.
9. Verify the network by pinging all remote networks and hosts.
Lab 5.3: Dynamic Routing with IGRP
In this lab, you will run the IGRP routing protocol simultaneously with RIP routing.
1. Log into your routers and go into privileged mode by typing en or enable.
2. Keep RIP running on your routers and verify that it is running on each router. If you want to remove RIP, you can use the no router rip
global configuration command to remove it from each router. For example,
config t
no router rip
3. From the configuration mode on Router A, type router igrp?
4. Notice that it asks for an autonomous system number. This is used to allow only routers with the same AS number to communicate. Type 10 and press Enter. Your router can be configured to be part of as many different ASs as necessary.
5. At the config-router prompt, type network 172.16.0.0. Notice that we add the classful network boundary to advertise rather than the subnet numbers.
6. Press Ctrl+Z to get out of configuration mode.
7. Go to Routers B and C and the 2621 router and type the commands shown here:
RouterB(config)#router igrp 10
RouterB(config-router)#network 172.16.0.0
8. Verify that IGRP is running by typing the following command at each router:
show ip protocol
Notice that this shows you your RIP and IGRP routing protocols and the update timers.
sh ip route
This should let you see all eight subnets: 10, 11, 15, 20, 30, 40, 50, and 55. Some will be directly connected, and some will be I routes, which are IGRP-injected routes. RIP is still running, but if you look at the routing table, you’ll notice the network entry has a network number (100/23456). The first number (100) is the trustworthiness rating. Since RIP’s default trustworthiness rating is 120, the IGRP route is used before a RIP route is used. The second number is the metric, or weight, of the route that is used to determine the best path to a network.
show running-config
This lets you see that RIP and IGRP are configured.
9. To save your configurations, type copy running-config startup-config or copy run start and press Enter at each router. Verify the network by pinging all routers, switches
Review Questions
1. What is the routing algorithm used by RIP?
- Routed information
- Link together
- Link state
- Distance vector
- Ans- distance vector
2. What is the routing algorithm used by IGRP?
- Routed information
- Link together
- Link state
- Distance vector
- Ans- distance vector
3. Which command can you type at the router prompt to verify the broadcast frequency for IGRP?
- sh ip route
- sh ip protocol
- sh ip broadcast
- debug ip igrp
- Ans- D
4. What is the routing metric used by RIP?
- Count to infinity
- Hop count
- TTL
- Bandwidth, delay
- Ans- B
5. What command is used to stop routing updates from exiting out an interface?
- Router(config-if)#no routing
- Router(config-if)#passive-interface
- Router(config-router)#passive-interface s0
- Router(config-router)#no routing updates
- Ans- D
6. What is the default routing metric used by IGRP? (Choose all that apply.)
- Count to infinity
- Hop count
- TTL
- Bandwidth
- Delay
- Ans- D , E
7. What does a metric of 16 hops represent in a RIP routing network?
- 16ms
- Number of routers in the internetwork
- Number of hops
- 16 hops—unreachable
- Last hop available
- Ans- D
8. What are hold-downs used for?
- To hold down the protocol from going to the next hop
- To prevent regular update messages from reinstating a route that has gone down
- To prevent regular update messages from reinstating a route that has just come up
- To prevent irregular update messages from reinstating a route that has gone down
- Ans- B
9. What is split horizon?
- When a router differentiates on which interface a packet arrived and does not advertise that information back out the same inter- face.
- When you have a large bus (horizon) physical network, it splits the traffic.
- It holds the regular updates from broadcasting to a downed
- It prevents regular update messages from reinstating a route that has gone
- Ans- A
10. What is poison reverse?
- It sends back the protocol received from a router as a poison pill, which stops the regular
- It is information received from a router that can’t be sent back to the originating
- It prevents regular update messages from reinstating a route that has just come
- It describes when a router sets the metric for a downed link to infinity.
- Ans- D
11. What is the default administrative distance for IGRP?
- 90
- 100
- 120
- 220
- Ans- B
12. Which of the following is a correct default route?
- route ip 172.0.0.0 255.0.0.0 s0
- ip route 0.0.0.0 0.0.0.0 172.16.20.1
- ip route 0.0.0.0 255.255.255.255 172.16.20.1
- route ip 0.0.0.0 0.0.0.0 172.16.10.1150
- Ans- A
13. Which of the following is an IP link state protocol?
- RIP V2
- EIGRP
- OSPF
- IGRP
- Ans- C
14. What commands are available for supporting RIP networks? (Choose all that apply.)
- sh ip route
- sh ip rip
- sh rip network
- debug ip rip
- Ans- B , D
15. Which of the following statements is true about distance-vector-based networks? (Choose the best answer.)
- They send out partial updates every 60
- They send their complete routing table every 60
- They send their entire routing table every 30
- They update every 90
- Ans- B
16. Which Cisco IOS command can you use to see the IP routing table?
- sh ip config
- sh ip arp
- sh ip route
- sh ip table
- Ans- C
17. What is the administrative distance used for in routing?
- Determining the network administrator for entering that route
- Creating a database
- Rating the source’s trustworthiness, expressed as a numeric value from 0 to 255
- Rating the source’s trustworthiness, expressed as a numeric value from 0 to 1023
- Ans- C
18. When looking at a routing table, what does the S mean?
- Dynamically connected
- Directly connected
- Statically connected
- Sending packets
- Ans- C
19. Which of the following is true about IP routing?
- The destination IP address changes at each
- The source IP address changes at each
- The frame does not change at each
- The frame changes at each
- Ans- D
20. Which of the following is true when creating static routes? (Choose all that apply.)
- The mask parameter is optional.
- The gateway parameter is required.
- The administrative distance is required.
- The administrative distance is optional.
- None of the
- Ans- B , C


