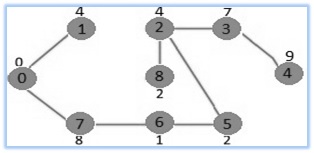
Prim’s Minimum Spanning Tree
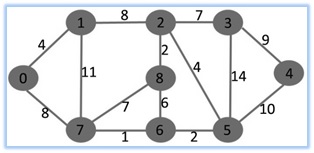
Prim’s Minimum Spanning Tree example
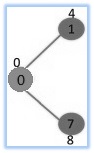
The set MST Set (minimum spanning tree set) is actually at first empty as well as keys assigned to vertices are 0, INF, INF, INF, INF, INF, INF, INF where INF signifies infinite. Now pick the vertex along with minimum key value. The vertex 0 is picked, consist of this within MST Set. Therefore MST Set becomes (0). Following such as in order to MST Set, update key values associated with adjacent vertices. Adjacent vertices associated with 0 are 1 and 7. The actual key values of 1 and 7 are updated as 4 and 8. Subsequent subgraph shows vertices as well as their own key values, only the vertices along with finite key values are shown.
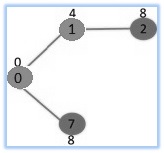
Select the vertex along with minimum key value and never currently contained in MST. The actual vertex 1 is picked as well as added to MST Set. Therefore MST Set now becomes (0, 1). Update the key values associated with adjacent vertices of 1. The actual key value associated with vertex 2 becomes 8.
Select the vertex along with minimum key value and never currently contained in MST. We could either choose vertex 7 or even vertex 2, let vertex 7 is picked. Therefore MST Set now becomes (0, 1, 7). Update the key values of adjacent vertices of 7. The key value associated with vertex 6 as well as 8 becomes finite (7 and 1 respectively).
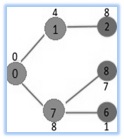
Select the vertex along with minimum key value and never currently contained in MST. Vertex 6 is picked. Therefore MST Set now becomes (0, 1, 7, 6). Update the key values associated with adjacent vertices of 6. The key value of vertex 5 and 8 tend to be updated.
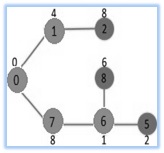
We repeat the above steps until MST Set consists of just about all vertices associated with given graph. Finally, we get the following graph.