Brent’s Algorithm Example
Operate the secant method to get the three roots with the cubic polynomial f[x] = 4x2 –16x2+17x-4.
Show information on the actual computations for that beginning value p0=3 and p1= 2.8
Solution:
Enter the function.
F[x_] = 4x3 -16x2 +17x -4
Print[{"f[x]="}, f[x]];
F[x] = -4+17x-16x2+4x2
The formula of secant iteration: g[x0, x1]
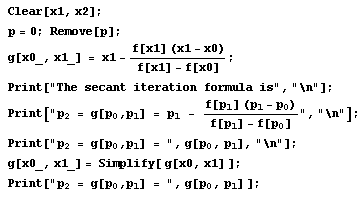
The formula of second iteration is,
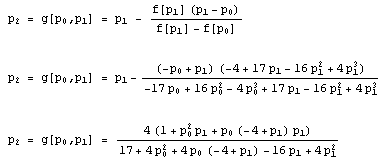
Hopefully, this iteration pn+1 = g[pn-1, pn] will probably converge into a root of f[x]. Graph this function y=f[x]
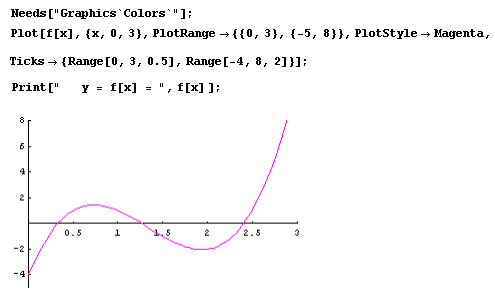
Y=f[x] = -4+17x-16x2+4x2
There are three kind real root.
Root(1) this root with starting the values p0=3.0 as well as p1=2.8.
Utilize the secant method to find a numerical approximation for the root Initial, do the iteration one step at the same time.
Kind each one of the subsequent commands inside an individual cell and execute these one-by-one.

Now use the subroutine.

In the graph we find that two other real roots.
Root(2) Use the starting values p0=0.6 and p1=0.5

Root(3) Use the starting values p0=1.0 and p1=1.1
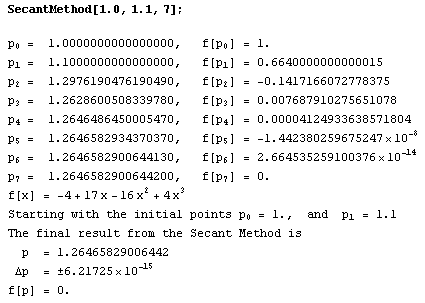
Evaluate the outcome along with Mathematica's built in numerical root finder.
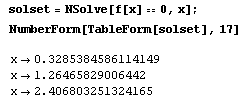
How they are good:

Mathematica may also solve for that roots symbolically.
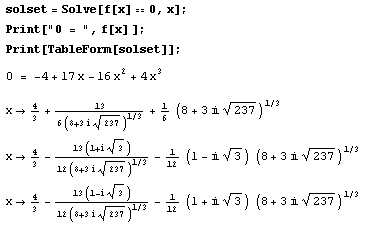
The actual solutions could be manipulated in to actual expressions.

The answers can be expressed in decimal form.

These answers are in agreement with the ones we found with the secant method.


