Asymptotic Analysis Algorithm Assignment Help
The primary concept of asymptotic analysis is actually to possess a way of measuring efficiency associated with algorithms which doesn’t rely on machine specific constants, as well as doesn’t need algorithms to become implemented and time taken by programs to be compared. Asymptotic notations tend to be mathematical tools in order to signify time complexity associated with algorithms with regard to asymptotic analysis. The next 3 asymptotic notations tend to be mainly representing time complexity associated with algorithms.
- Θ Notation
- Big O Notation
- Ω Notation
Θ Notation:
The theta notation bounds a function, therefore it identifies exact asymptotic behavior.
Therefore it identifies Theta notation of the phrase would be to drop low order conditions as well as ignore leading constants. For instance, consider the following expression.
3n3 + 6n2 + 6000 = Θ(n3)
Dropping lower order terms is definitely good simply because there will be always be a n0 after which it Θ(n3) beats Θn2) regardless of the actual constants included. For any given perform g(n), all of us signify Θ(g(n)) is actually subsequent set associated with functions.

This is signifies, when f(n) will be theta of g(n), then a value f(n) is definitely in between c1*g(n) as well as c2*g(n) with regard to large values associated with n (n >= n0). The meaning associated with theta also requires that f(n) should be non-negative with regard to ideals associated with n more than n0.
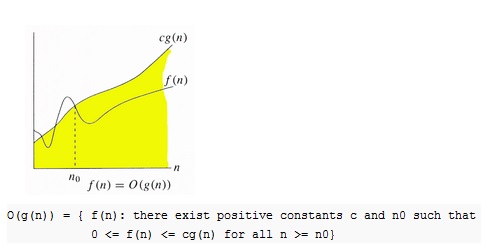
Big O Notation:
The Big O notation identifies an upper bound of an algorithm, this range the function. For instance, consider the case associated with Insertion Sort. It requires linear time in best case as well as quadratic time in worst case. we areable to properly state how the time complexity associated with Insertion sort is O(n^2).
O(n^2) additionally handles linear time.
In the event that all of us use Θ notation in order to signify period complexity associated with Insertion sort, we must make use of two statements with regard to best as well as worst cases:
- The worst case time complexity of Insertion Sort is Θ(n^2).
- The best case time complexity of Insertion Sort is Θ(n).
The Big O notation is useful whenever we just possess upper bound on time complexity of an algorithm. Many times we easily find an upper bound by simply looking at the algorithm.
Ω Notation:
Big O notation has an asymptotic upper bound on a function, Ω notation has an asymptotic lower bound.
Ω Notation < can be useful whenever we possess lower bound on time complexity of an algorithm. The actual best case overall performance of the algorithm is usually not really helpful, the Omega notation may be the minimum utilized notation among all three.
For a given function g(n), all of us signify through Ω(g(n)) the group of features.

The actual time complexity associated with Insertion Sort could be created because Ω(n), however it's not an extremely helpful details about insertion sort, as we aregenerally interested in worst case as well as sometimes in average case.


