Bounded Set, Compact Set and Connected Subsets of R
Bounded Set
A set A ⊂ R is bounded from above if there exists a number K such that
x ≤ K ∀ x ∈ A
K is called the upper bound of A. Every number greater than K is also an upper bound of A.
A set A ⊂ R is bounded from below if there exists a number k such that
k ≤ x ∀ x ∈ A
k is called the lower bound of A. Every number smaller then k is also a lower bound of A.
A set is called a bounded set if it is bounded from above as well as from below. Thus the set A is a bounded set if there exist k and K such that
k ≤ x ≤ K ∀ x ∈ A or A ⊂ [k,K]
The bounds of a set may or may not belong to the set.
The upper bound of set which belongs to the set is called its greatest member. A lower bound of a set which belongs to the set is called its smallest member. A set may or may not have greatest and smallest members.
The set of upper bounds of a set which is bounded above has a smallest members called the least upper bound or the Supremum of set denoted by Sup A or M.
The set of lower bounds of a set which is bounded below has a greatest member called the greatest lower bound of Infimum of set denotes by Inf A or m.
M and m may or may not belong to the set.
- [a,b] is bounded set with m = a and M = b.
- a is also the smallest member and b is the greatest member of [a,b]
- (a,b] is bounded set with m = a and M = b
- a is not the smallest member and b is the greatest member of (a,b]
- [a,b) is bounded set with m = a and M = b
- a is the smallest member and b is not greatest member of [a,b).
- (a,b) is bounded set with m = a and M = b
- a is not the smallest member and b is not the greatest member of (a,b)
| Subset of R | Bounded or not? | Infimum of set (m) | Supremum of set (M) | Whether ‘a’ is the smallest member of set? | Whether ‘b’ is the greatest member of set? |
|---|---|---|---|---|---|
| [a,b] | Bounded | A | b | a is the smallest member of [a,b] | b is the greatest member of [a,b] |
| (a,b] | Bounded | A | b | NO | b is the greatest member of (a,b] |
| [a,b) | Bounded | A | b | a is the smallest member of [a,b] | NO |
| (a,b) | Bounded | A | b | NO | NO |
The set of natural numbers ‘N’ is bounded from below but is not bounded from above. 1 is the infimum of set of natural numbers as well as the smallest member of the set of Natural numbers.
The set of whole numbers ‘W’ is bounded from below but is not bounded from above. 0 is the infimum of the set of whole numbers as well as the smallest member of the set of Whole numbers.
The set of Integers ‘Z’ is not bounded set.
Every finite set is bounded set.
The set of rational numbers Q is not bounded set.
The set of real numbers R is not bounded set.
Open Cover of a set
Let A ⊂ R. An open cover of A is collection of {A_λ: λ∈Λ} of open sets in R whose union contains A, i.e.,
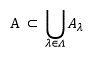
A sub collection of {Aλ: λ ∈ Λ} which also covers A is called subcover of {Aλ: λ ∈ Λ}
A subcover which contains finite number of open sets is called finite subcover of {Aλ: λ ∈ Λ}
e.g. Let A = [2, ∞)
Consider A1 = {(1, ∞)}
A2 = {(n-1, n+1) : n ∈ N } = {(0,2), (1,3), (2,4), (3,5), … }
A3 = {(0, n) : n ∈ N} = {(0, 1), (0, 2), (0, 3), (0, 4), … }
A4 = {(0, n): n ∈ N, 10 ≤ n} = {(0, 10), (0, 11), (0, 12), … }
A1, A2, A3, A4 are all open covers of A. A4 is the subcover of A3. Also A1 having only one member is finite cover of A.
Compact Set
A subset K ⊂ R is said to be a compact set if every open cover of K has a finite subcover.
Thus, K is compact set if whenever it is contained in the union of a collection A of open set in R, then it is contained in the union of some finite number of sets in A. K is not compact set if there exists even one open cover of K which has no finite subcover.
The necessary and sufficient condition for a subset of R to be compact set is defined by the Heine-Borel Theorem:
Heine - Borel Theorem: A subset K of R is compact set if and only if it is closed set and bounded set.
This theorem describes all the compact subsets of R.
Every finite set being closed set and bounded set is compact set.
Consider K = {a1 ,a2,…,an } a finite subset of R.
Let A = {Aλ: λ ∈ Λ} be an open cover of K
i.e. , K ⊂ ⋃λ∈ΛAλ
Now each ai ∈ Aλi for some Aλi ∈ A
Now union of { Aλ1 ,Aλ2,…,Aλn } contains K and hence it is a finite subcover of A
So every open cover of K has a finite subcover so by definition K is compact.
[a,b] is compact set but (a,b] , [a,b), (a,b) are not compact set
The set of all rational numbers Q is neither closed set nor bounded set therefore Q is not compact set.
Since the set of all real numbers R is not bounded set therefore R is not compact set.
Since the set of all natural numbers N is not bounded set therefore N is not compact set.
{1/n ∶n ∈ N } is not compact set as it is not closed set.
If K ⊂ R is compact set and x ∈ K then we can find two open sets A and B such that
- x ∈ A
- K ⊂ B
- A ∩ B = ∅
Connected Sets
A set S ⊂ R is disconnected set if there exists open sets A and B such that
- S ⊂ A ∪ B
- S ∩ A ≠ ∅ and S ∩ B ≠ ∅
- A ∩ B = ∅
In other words, S is disconnected set if it can be broken onto two non-empty sets such that the two parts are respectively contained in two disjoint sets,
If S is not disconnected set, then we can say that S is connected set.
The connected sets in R can be characterized by the following theorem:
Theorem: A subset S of R is connected if and only if whenever a,b ∈ S and a< c < b then c ∈ S
All the intervals [a,b], (a,b), [a,b), (a,b], (-∞,a) and (a, ∞) are connected set.
The set of all real numbers R = (-∞,∞) is also connected set.
A finite subset of R is disconnected set.
The set of rational numbers Q is disconnected set as :
- Q ⊂(-∞,√2) ∪ (√2,∞) = R - {√2 }
- Q ∩(-∞,√2) ≠ ∅, Q ∩(√2,∞) ≠ ∅
- (-∞,√2) ∩ (√2,∞) = ∅
The set of all integers Z is not connected set.
For more information on bounded sets in real analysis, connected sets proofs and help with compact sets in topology and other real analysis topics, schedule a Math live tutoring session with our MathHelp service.


