Suffix Array
1. Suffix Array Introduction
String matching is a basic step used by mostly algorithms. And for exact String matching, Let’s say you have an array namely S[1…..n] and you need to search a pattern P, say m length. Then for performing exact string matching algorithm, it will take O(m + n) time. What we do to reduce this time. We generally do pre-processing of the text. Pre-processing make the time complexity linear.
Suffix array is a way of doing this pre-processing. Suffix Array is an array based data structure which contains all the suffixes of a string. The elements are sorted lexicographically. It is mainly used in Data compression algorithms and in the field of Bio-informatics.
Manber & Myers in 1990 developed the concept of Suffix arrays. The idea was to provide an alternative to Suffix Tree which is another data structure used for pattern matching algorithm. Suffix Arrays are space efficient as compared to suffix tree.
2. Constructing Algorithms
Since, Suffix array is a data structure and for pattern matching, we need to see it’s use by implementing some algorithms.
So, in this section, we’ll explore some ways of using Suffix arrays. Let’s get started.
What we want with suffix array: We’ll explain the answer with an example
Let’say we have a string S=attcatg. First we’ll create suffix array and then we’ll sort it.
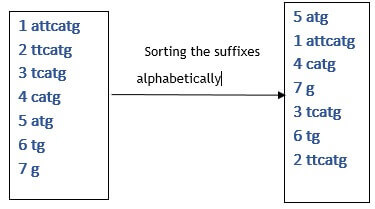
We need to do this task which is presented in the above picture. The left box contains the suffixes which can be obtained by the original string and the right side is its suffix array.
Firstly, we’ll implement the most naïve algorithm which can solve our problem. We need to sort suffixes of a string in lexicographical order, for that we need a good comparison based sorting algorithm and Quick sort is a good option.
Now, We’ll discuss the time complexity for this approach.
Since, we are using quick sort. Its complexity is O(n log n). And also for pattern matching, it will take O(n) time. So the overall time complexity for this will be O(n^2 log n).
In order to retrieve the original array after sorting all the sub strings, we need to maintain the sub-string’s order. For that purpose, there should be indices along with each substring. So, that we’ll be able to obtain the initial array. For doing this task, we’ll use maps where substrings will act as the keys and the indexes given in the original array would be the values, mapped with these keys. This will make our task of maintaining the order easy.
Below, we’ll show the implementation of this algorithm.
3. Implementation in C++
{`
#include < iostream.h>
#include < string.h>
#include < map>
#include < algorithm>
#include < vector>
using namespace std;
int main()
string a;
map< string,int> m;
cin >> a; // prompting user to enter the string
vector< string> b;
for(int i = 0; i < a.size();i++)
m[a.substr(i,a.size()-i)] = i; //creating substrings
b.push_back(a.substr(i,a.size()-i));
sort(b.begin(),b.end()); // sorting the substrings
for(int i = 0; i < b.size();i++)
cout << m[b[i]] << endl;
return 0;
`}
In above implementation, we used built-in functions which made the task easier. But that’ll increase the time complexity, making it practically impossible to implement.
So, we cannot implement this approach.
Now, we’ll try something smarter. Since the suffix array is constituted with a single string. So, we can exploit this fact to reduce the time complexity.
For this purpose, we’ll use tuples for comparing. We’ll compare the characters in power of 2.
We’ll start by taking firstly two characters and then the strings which have same characters will get same index, let’s name this index as ‘cmp index’. So, In first round we’ll get the list of sub-strings sorted on the basis of first two characters.
Then, we’ll make the count 4 and repeat the above written procedure. We keep continuing this until the strings are completely sorted.
So, with this approach, the running time for constructing Suffix Array will get reduced from
O(N2 log N) to O(N log2 N).
Let’s understand the above written procedure with an example.
Suppose we have a string ‘mississippi’. We want to create its suffix array.
{`
Index Substrings
0 mississippi
1 ississippi
2 ssissippi
3 sissippi
4 issippi
5 ssippi
6 sippi
7 ippi
8 ppi
9 pi
10 i
This is the unsorted array
`}
In the above diagram, we have mentioned the substrings along with their indexes. In next diagram, we’ll assign ‘cmp index’ along with their original index.
{`
Cmp-Index Index: substrings
0 10: i
1 7: ippi
2 1: ississippi
2 4: issippi
3 0: mississippi
4 9: pi
5 8: ppi
6 3: sissippi
6 6: sippi
7 2: ssissippi
7 5: ssippi
`}
In the above diagram, we wrote Cmp-indexes along with the original indexes. As we explained earlier, the sub strings which have same first two characters will possess same Cmp-index.
{`
Cmp-Index2 Index: Substring Tuple 1
0 10: i -1 (0, -1)
1 7: ippi 9 (1, 4)
2 1: ississippi 3 (2, 6)
2 4: issippi 6 (2, 6)
3 0: mississippi 2 (3, 7)
4 9: pi -1 (4, -1)
5 8: ppi 10 (5, 0)
6 3: sissippi 5 (6, 7)
6 6: sippi 8 (6, 5)
7 2: ssissippi 4 (7, 2)
7 5: ssippi 7 (7, 1)
`}
In the above diagram, we used tuples of 2 values, first value is the Cmp index of the substring and the second value is the Cmp Index2, which is the sorting index for first four characters.
The substrings which have less than 4 character, we assigned them -1 value.
After getting the above array, we’ll apply quick sort by using the tuples- 2 we created above for obtaining the suffix array.
{`
Cmp Index Index : sub-strings
0 10: i
1 7: ippi
2 1: ississippi
2 4: issippi
3 0: mississippi
4 9: pi
5 8: ppi
6 3: sissippi
7 6: sippi
8 2: ssissippi
9 5: ssippi
`}
In the above diagram, we achieved the Array sorted on the basis of first four characters.
After this, we’ll sort them for 8 characters. Then we’ll create the tuples similarly as above and after applying quick sort again, we’ll get the suffix array.
Thus, we can obtain the suffix array by implementing the pseudocode written below:
{`
SortIndex[][] = { 0 }
for i = 0 to N-1
SortIndex[0][i] = order index of the character at A[i]
doneTill = 1
step = 1
while doneTill < N
L[] = { (0,0,0) } // Array of 3 tuples
for i = 0 to N-1
L[i] = ( SortIndex[step - 1][i],
SortIndex[step - 1][i + doneTill],
i
)
// We keep the values of ‘i’ for getting the original index
sort L
for i = 0 to N-1
SortIndex[step][L[i].thirdValue] =
SortIndex[step][L[i-1].thirdValue], if L[i] and L[i-1] have the same first and second values
i, otherwise
++step
doneTill *= 2
`}
The time complexity of implementation of above code will be O(n log^2 n).
Below we have implemented the above pesudcode in C++.
Program in C++
{`
#include < cstdio>
#include < algorithm>
#include < cstring>
using namespace std;
#define MAXN 65536
#define MAXLG 17
char A[MAXN];
struct entry
L[MAXN];
int P[MAXLG][MAXN];
int N,i;
int stp, cnt;
int cmp(struct entry a, struct entry b)
L[i].nr[0]=P[stp- 1][i];
L[i].nr[1]=i +cnt < N? P[stp -1][i+ cnt]:-1;
L[i].p= i;
sort(L, L+N, cmp);
for(i=0; i < N; i++)
P[stp][L[i].p] =i> 0 && L[i].nr[0]==L[i-1].nr[0] && L[i].nr[1] == L[i- 1].nr[1] ? P[stp][L[i-1].p] : i;
`}
Now, we are introducing another concept that is Longest Common Prefixes also called LCP array.
It’ll make our task easier. If we have developed the suffix array, then building LCP array is relatively easier. LCP array is an auxiliary data structure which is used to store the length of longest common prefixes using the pairs of consecutive suffixes contained in suffix array, as an input.
We’ll be using our cmp-index and cmp index2 for constructing LCP array. To make our task easier, we’ll name it as SortIndex.
{`
FindLCP (x, y)
answer = 0
for k = ceil(log N) to 0
if SortIndex[k][x] = SortIndex[k][y]
// sort-index is same if the first k characters are same
answer += 2k
// now we wish to find the characters that are same in the remaining strings
x += 2k
y += 2k
`}
There are many other algorithms which can make the procedure we did above a lot easier. Skew algorithms are one of them.
4. Suffix Array Vs. Suffix Tree
Suffix array can be defined as a data structure which is space-efficient. If it is stored together with the original string, then it provides the same functions as a suffix tree.
We can think of suffix array as a storage mechanism for suffix trees. Depending on the value of other parameters, the performance costs may be there in case of using arrays over full-blown trees which are typically are outweighed by the space-use benefits.
The Suffix arrays are the preferred method for storing or representing a suffix tree.


